Routing (hydrology)

From Wikipedia, the free encyclopedia

In hydrology, routing is a technique used to predict the changes in shape of water as it moves through a river channel or a reservoir. In flood forecasting, hydrologists may want to know how a short burst of intense rain in an area upstream of a city will change as it reaches the city. Routing can be used to determine whether the pulse of rain reaches the city as a deluge or a trickle. Other uses of routing include reservoir and channel design, floodplain studies and watershed simulations.[1]

If the water flow at a particular point, A, in a stream is measured over time with a flow gauge, this information can be used to create a hydrograph. A short period of intense rain, normally called a flood event, can cause a bulge in the graph, as the increased water travels down the river, reaches the flow gauge at A, and passes along it.

If another flow gauge at B, downstream of A is set up, one would expect the bulge (or floodwave) to have the same shape. However, the shape of the river and flow resistance within a river (from the river bed, for example) can affect the shape of the floodwave. Oftentimes, the floodwave will be attenuated (have a reduced peak flow).

Routing techniques can be broadly classified as following:

Hydraulic (or distributed) routing

Hydraulic routing is based on the solution of partial differential equations of unsteady open-channel flow. The equations used are the St. Venant equations or the dynamic wave equations.[2][3]

The hydraulic models (e.g. dynamic and diffusion wave models) require the gathering of a lot of data related to river geometry and morphology and consume a lot of computer resources in order to solve the Saint-Venant equations numerically.[4][5][6]

Hydrologic (or lumped) routing

Hydrologic routing uses the continuity equation for hydrology. In its simplest form, inflow to the river reach is equal to the outflow of the river reach plus the change of storage:

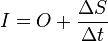I=O+{\frac {\Delta S}{\Delta t}}, where
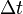
  • I is average inflow to the reach during \Delta t
  • O is average outflow from the reach during 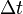\Delta t; and
  • S is the water currently in the reach (known as storage)

The hydrologic models (e.g. linear and nonlinear Muskingum models) need to estimate hydrologic parameters using recorded data in both upstream and downstream sections of rivers and/or by applying robust optimization techniques to solve the one dimensional conservation of mass and storage-continuity equation.[7]

Semi-distributed routing

Nowadays, semi-distributed models such as Muskingum–Cunge family procedures are also available. Simple physically concepts and common river characteristic consist of channel geometry, reach length, roughness coefficient, and slope are used to estimate the model parameters without complex and expensive numerical solutions.[8][9][10]

Selection of routing procedure

In general, based on the available field data and goals of the project, one of routing procedures is selected.

See also

References

  1. ↑ EM 1110-2-1417 (1994). "Chapter 9 - Streamflow and Reservoir Routing". Flood Run-off Analysis. U.S. Army Corps of Engineers. p. 9-1. 
  2. ↑ Chow V. T, Maidment D. R, Mays L.W (1988). Applied Hydrology. McGraw1Hill International Editions: Singapore.
  3. ↑ Akan A. O (2006). Open Channel Hydraulics. Elsevier, New York, NY, USA.
  4. ↑ Chaudhry MH (1993) Open-Channel Flow. Prentice Hall, Englewood Cliffs, NJ, USA.
  5. ↑ Samani H. M. V, Shamsipour G. A (2004). Hydrologic flood routing in branched river systems via nonlinear optimization. Journal of Hydraulic Research, 42(1): 55-59.
  6. ↑ Akbari G. H, Barati R (2012). Comprehensive analysis of flooding in unmanaged catchments. Proceedings of the Institution of Civil Engineers-Water Management, 165(4): 229-238.
  7. ↑ Barati R (2011). Parameter estimation of nonlinear Muskingum models using Nelder-Mead Simplex algorithm. Journal of Hydrologic Engineering, 16(11): 946-954.
  8. ↑ Cunge J. A (1969). On the subject of a flood propagation computational method (Muskingum method). Journal of Hydraulic Research, 7(2): 2051230.
  9. ↑ Perumal M (1994). Hydrodynamic derivation of a variable parameter Muskingum method: 1. Theory and solution procedure. Hydrological sciences journal, 39(5): 431–442.
  10. ↑ Barati R, Akbari GH and Rahimi S (2013) Flood routing of an unmanaged river basin using Muskingum–Cunge model; field application and numerical experiments. Caspian Journal of Applied Sciences Research, 2(6):08-20.
This article is issued from Wikipedia. The text is available under the Creative Commons Attribution/Share Alike; additional terms may apply for the media files.