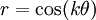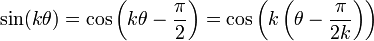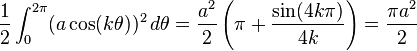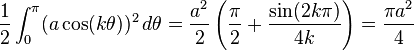Rose (mathematics)

From Wikipedia, the free encyclopedia

For the topological usage, see Rose (topology).

Rose with k = 7 petals

Rose with 8 petals (k=4).

Rose curves defined by $r=\cos k\theta$ , for various values of k=n/d.

In mathematics, a rose or rhodonea curve is a sinusoid plotted in polar coordinates.

General overview

Up to similarity, these curves can all be expressed by a polar equation of the form

$\!\,r=\cos(k\theta )$

or, alternatively, as a pair of Cartesian parametric equations of the form

$\!\,x=\cos(kt)\sin(t)$

$\!\,y=\cos(kt)\cos(t)$

If k is an integer, the curve will be rose shaped with

2k petals if k is even, and
k petals if k is odd.

When k is even, the entire graph of the rose will be traced out exactly once when the value of θ changes from 0 to 2π. When k is odd, this will happen on the interval between 0 and π. (More generally, this will happen on any interval of length 2π for k even, and π for k odd.)

If k ends in 1/2 (ex: 0.5, 2.5), the curve will be rose shaped with 4k petals.

If k ends in 1/6 or 5/6 and is greater than 1 (ex: 1.16666667, 2.8333333), the curve will be rose shaped with 12k petals.

If k ends in 1/3 and is greater than 1 (ex: 1.333333, 2.333333), the curve will be rose shaped and will have:

3k petals if k is even, and
6k petals if k is odd.

If k ends in 2/3 and is greater than 1 (ex: 1.666667, 2.666667), the curve will be rose shaped and will have:

6k petals if k is even, and
3k petals if k is odd.

If k is rational, then the curve is closed and has finite length. If k is irrational, then it is not closed and has infinite length. Furthermore, the graph of the rose in this case forms a dense set (i.e., it comes arbitrarily close to every point in the unit disk).

Since

$\sin(k\theta )=\cos \left(k\theta -{\frac {\pi }{2}}\right)=\cos \left(k\left(\theta -{\frac {\pi }{2k}}\right)\right)$

for all 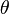$\theta$ , the curves given by the polar equations

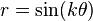$\,r=\sin(k\theta )$ and $\,r=\cos(k\theta )$

are identical except for a rotation of π/2k radians.

Rhodonea curves were named by the Italian mathematician Guido Grandi between the year 1723 and 1728.^[1]

Area

A rose whose polar equation is of the form

$r=a\cos(k\theta )\,$

where k is a positive integer, has area

${\frac {1}{2}}\int _{{0}}^{{2\pi }}(a\cos(k\theta ))^{2}\,d\theta ={\frac {a^{2}}{2}}\left(\pi +{\frac {\sin(4k\pi )}{4k}}\right)={\frac {\pi a^{2}}{2}}$

if k is even, and

${\frac {1}{2}}\int _{{0}}^{{\pi }}(a\cos(k\theta ))^{2}\,d\theta ={\frac {a^{2}}{2}}\left({\frac {\pi }{2}}+{\frac {\sin(2k\pi )}{4k}}\right)={\frac {\pi a^{2}}{4}}$

if k is odd.

The same applies to roses with polar equations of the form

$r=a\sin(k\theta )\,$

since the graphs of these are just rigid rotations of the roses defined using the cosine.

How the parameter k affects shapes

In the form k = n, for integer n, the shape will appear similar to a flower. If n is odd half of these will overlap, forming a flower with n petals. However if it is even the petals will not overlap, forming a flower with 2n petals.

When d is a prime number then n/d is a least common form and the petals will stretch around to overlap other petals. The number of petals each one overlaps is equal to the how far through the sequence of primes this prime is +1, i.e. 2 is 2, 3 is 3, 5 is 4, 7 is 5, etc.

In the form k = 1/d when d is even then it will appear as a series of d/2 loops that meet at 2 small loops at the center touching (0, 0) from the vertical and is symmetrical about the x-axis. If d is odd then it will have d div 2 loops that meet at a small loop at the center from ether the left (when in the form d = 4n − 1) or the right (d = 4n + 1).

If d is not prime and n is not 1, then it will appear as a series of interlocking loops.

If k is an irrational number (e.g. $\pi$ , ${\sqrt {2}}$ , etc.) then the curve will have infinitely many petals, and it will be dense in the unit disc.

Notes

↑ O'Connor, John J.; Robertson, Edmund F., "Rhodonea", MacTutor History of Mathematics archive, University of St Andrews .

External links

Wikimedia Commons has media related to Rose curves.

This article is issued from Wikipedia. The text is available under the Creative Commons Attribution/Share Alike; additional terms may apply for the media files.