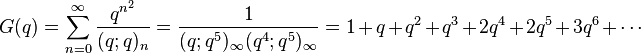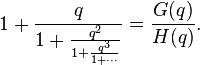Rogers–Ramanujan identities

From Wikipedia, the free encyclopedia

In mathematics, the Rogers–Ramanujan identities are two identities related to basic hypergeometric series, first discovered and proved by Leonard James Rogers (1894). They were subsequently rediscovered (without a proof) by Srinivasa Ramanujan some time before 1913. Ramanujan had no proof, but rediscovered Rogers's paper in 1917, and they then published a joint new proof (Rogers & Ramanujan 1919). Issai Schur (1917) independently rediscovered and proved the identities.

Definition

The Rogers–Ramanujan identities are

$G(q)=\sum _{{n=0}}^{\infty }{\frac {q^{{n^{2}}}}{(q;q)_{n}}}={\frac {1}{(q;q^{5})_{\infty }(q^{4};q^{5})_{\infty }}}=1+q+q^{2}+q^{3}+2q^{4}+2q^{5}+3q^{6}+\cdots \,$ (sequence A003114 in OEIS)

and

$H(q)=\sum _{{n=0}}^{\infty }{\frac {q^{{n^{2}+n}}}{(q;q)_{n}}}={\frac {1}{(q^{2};q^{5})_{\infty }(q^{3};q^{5})_{\infty }}}=1+q^{2}+q^{3}+q^{4}+q^{5}+2q^{6}+\cdots \,$ (sequence A003106 in OEIS).

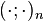Here, $(\cdot ;\cdot )_{n}$ denotes the q-Pochhammer symbol.

Modular functions

If q = e^2πiτ, then q^−1/60G(q) and q^11/60H(q) are modular functions of τ.

Applications

The Rogers–Ramanujan identities appeared in Baxter's solution of the hard hexagon model in statistical mechanics.

Ramanujan's continued fraction is

$1+{\frac {q}{1+{\frac {q^{2}}{1+{\frac {q^{3}}{1+\cdots }}}}}}={\frac {G(q)}{H(q)}}.$

References

Rogers, L. J.; Ramanujan, Srinivasa (1919), "Proof of certain identities in combinatory analysis.", Cambr. Phil. Soc. Proc. 19: 211–216, Reprinted as Paper 26 in Ramanujan's collected papers
Rogers, L. J. (1892), "On the expansion of some infinite products", Proc. London Math. Soc. 24 (1): 337–352, doi:10.1112/plms/s1-24.1.337, JFM 25.0432.01
Rogers, L. J. (1893), "Second Memoir on the Expansion of certain Infinite Products", Proc. London Math. Soc. 25 (1): 318–343, doi:10.1112/plms/s1-25.1.318
Rogers, L. J. (1894), "Third Memoir on the Expansion of certain Infinite Products", Proc. London Math. Soc. 26 (1): 15–32, doi:10.1112/plms/s1-26.1.15

Issai Schur, Ein Beitrag zur additiven Zahlentheorie und zur Theorie der Kettenbrüche, (1917) Sitzungsberichte der Berliner Akademie, pp. 302–321.
W.N. Bailey, Generalized Hypergeometric Series, (1935) Cambridge Tracts in Mathematics and Mathematical Physics, No.32, Cambridge University Press, Cambridge.
George Gasper and Mizan Rahman, Basic Hypergeometric Series, 2nd Edition, (2004), Encyclopedia of Mathematics and Its Applications, 96, Cambridge University Press, Cambridge. ISBN 0-521-83357-4.
Bruce C. Berndt, Heng Huat Chan, Sen-Shan Huang, Soon-Yi Kang, Jaebum Sohn, Seung Hwan Son, The Rogers-Ramanujan Continued Fraction, J. Comput. Appl. Math. 105 (1999), pp. 9–24.
Cilanne Boulet, Igor Pak, A Combinatorial Proof of the Rogers-Ramanujan and Schur Identities, Journal of Combinatorial Theory, Ser. A, vol. 113 (2006), 1019–1030.
Slater, L. J. (1952), "Further identities of the Rogers-Ramanujan type", Proceedings of the London Mathematical Society. Second Series 54 (2): 147–167, doi:10.1112/plms/s2-54.2.147, ISSN 0024-6115, MR 0049225

External links

This article is issued from Wikipedia. The text is available under the Creative Commons Attribution/Share Alike; additional terms may apply for the media files.