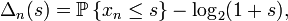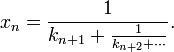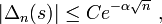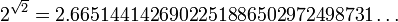Rodion Kuzmin

From Wikipedia, the free encyclopedia

Rodion Kuzmin
Rodion Kusmin, circa 1926
Born	(1891-10-09)9 October 1891 Riabye village in the Haradok district
Died	April 23, 1949(1949-04-23) (aged 57) Leningrad
Nationality	Russian
Fields	Mathematics
Institutions	Perm State University, Tomsk Polytechnic University, Saint Petersburg State Polytechnical University
Alma mater	Saint Petersburg State University nee Petrograd University
Doctoral advisor	James Victor Uspensky
Known for	Gauss–Kuzmin distribution, number theory and mathematical analysis.

Rodion Osievich Kuzmin (Russian: Родион Осиевич Кузьмин, Nov. 9, 1891, Riabye village in the Haradok district – March 23, 1949, Leningrad) was a Russian mathematician, known for his works in number theory and analysis.^[1]

Selected results

In 1928, Kuzmin solved^[2] the following problem due to Gauss (see Gauss–Kuzmin distribution): if x is a random number chosen uniformly in (0, 1), and

$x={\frac {1}{k_{1}+{\frac {1}{k_{2}+\cdots }}}}$

is its continued fraction expansion, find a bound for

$\Delta _{n}(s)={\mathbb {P}}\left\{x_{n}\leq s\right\}-\log _{2}(1+s),$

where

$x_{n}={\frac {1}{k_{{n+1}}+{\frac {1}{k_{{n+2}}+\cdots }}}}.$

Gauss showed that Δ_n tends to zero as n goes to infinity, however, he was unable to give an explicit bound. Kuzmin showed that

$|\Delta _{n}(s)|\leq Ce^{{-\alpha {\sqrt {n}}}}~,$

where C,α > 0 are numerical constants. In 1929, the bound was improved to C 0.7ⁿ by Paul Lévy.

In 1930, Kuzmin proved^[3] that numbers of the form a^b, where a is algebraic and b is a real quadratic irrational, are transcendental. In particular, this result implies that Gelfond–Schneider constant

$2^{{{\sqrt {2}}}}=2.6651441426902251886502972498731\ldots$

is transcendental. See Gelfond–Schneider theorem for later developments.

Notes

↑ Venkov, B. A.; Natanson, I. P.. "R. O. Kuz’min (1891–1949) (obituary)". Uspekhi matematicheskikh nauk 4 (4): 148–155.
↑ Kuzmin, R.O. (1928). "On a problem of Gauss". DAN SSSR: 375–380.
↑ Kuzmin, R. O. (1930). "On a new class of transcendental numbers". Izvestiya Akademii Nauk SSSR (math.) 7: 585–597.

External links

Rodion Kuzmin at the Mathematics Genealogy Project (The chronology there is apparently wrong, since J. V. Uspensky lived in USA from 1929.)

Persondata
Name	Kuzmin, Rodion
Alternative names
Short description	Russian mathematician
Date of birth	October 9, 1891
Place of birth	Riabye village in the Haradok district
Date of death	April 23, 1949
Place of death	Leningrad

This article is issued from Wikipedia. The text is available under the Creative Commons Attribution/Share Alike; additional terms may apply for the media files.