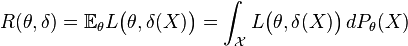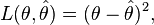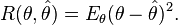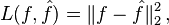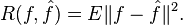Risk function

From Wikipedia, the free encyclopedia

This article is about the mathematical definition of risk in statistical decision theory. For a more general discussion of concepts and definitions of risk, see the main article Risk.

In decision theory and estimation theory, the risk function R of a decision rule δ, is the expected value of a loss function L:

$R(\theta ,\delta )={{\mathbb E}}_{\theta }L{\big (}\theta ,\delta (X){\big )}=\int _{{\mathcal {X}}}L{\big (}\theta ,\delta (X){\big )}\,dP_{\theta }(X)$

where

θ is a fixed but possibly unknown state of nature;
X is a vector of observations stochastically drawn from a population;
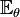${{\mathbb E}}_{\theta }$ is the expectation over all population values of X;
dP_θ is a probability measure over the event space of X, parametrized by θ; and
the integral is evaluated over the entire support of X.

Examples

For a scalar parameter θ, a decision function whose output ${\hat \theta }$ is an estimate of θ, and a quadratic loss function

$L(\theta ,{\hat \theta })=(\theta -{\hat \theta })^{2},$

the risk function becomes the mean squared error of the estimate,

$R(\theta ,{\hat \theta })=E_{\theta }(\theta -{\hat \theta })^{2}.$

In density estimation, the unknown parameter is probability density itself. The loss function is typically chosen to be a norm in an appropriate function space. For example, for L² norm,

$L(f,{\hat f})=\|f-{\hat f}\|_{2}^{2}\,,$

the risk function becomes the mean integrated squared error

$R(f,{\hat f})=E\|f-{\hat f}\|^{2}.\,$

References

Nikulin, M. S. (2001), "Risk of a statistical procedure", in Hazewinkel, Michiel, Encyclopedia of Mathematics, Springer, ISBN 978-1-55608-010-4
Berger, James O. (1985). Statistical decision theory and Bayesian Analysis (2nd ed.). New York: Springer-Verlag. ISBN 0-387-96098-8. MR 0804611.
DeGroot, Morris (2004) [1970]. Optimal Statistical Decisions. Wiley Classics Library. ISBN 0-471-68029-X. MR 2288194.
Robert, Christian P. (2007). The Bayesian Choice (2nd ed.). New York: Springer. doi:10.1007/0-387-71599-1. ISBN 0-387-95231-4. MR 1835885.

This article is issued from Wikipedia. The text is available under the Creative Commons Attribution/Share Alike; additional terms may apply for the media files.