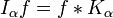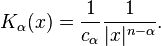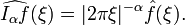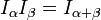Riesz potential

From Wikipedia, the free encyclopedia

In mathematics, the Riesz potential is a potential named after its discoverer, the Hungarian mathematician Marcel Riesz. In a sense, the Riesz potential defines an inverse for a power of the Laplace operator on Euclidean space. They generalize to several variables the Riemann–Liouville integrals of one variable.

If 0 < α < n, then the Riesz potential I_αf of a locally integrable function f on Rⁿ is the function defined by

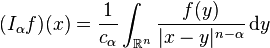
$(I_{{\alpha }}f)(x)={\frac {1}{c_{\alpha }}}\int _{{{{\mathbb {R}}}^{n}}}{\frac {f(y)}{|x-y|^{{n-\alpha }}}}\,{\mathrm {d}}y$

(1)

where the constant is given by

$c_{\alpha }=\pi ^{{n/2}}2^{\alpha }{\frac {\Gamma (\alpha /2)}{\Gamma ((n-\alpha )/2)}}.$

This singular integral is well-defined provided f decays sufficiently rapidly at infinity, specifically if f ∈ L^p(Rⁿ) with 1 ≤ p < n/α. If p > 1, then the rate of decay of f and that of I_αf are related in the form of an inequality (the Hardy–Littlewood–Sobolev inequality)

$\|I_{\alpha }f\|_{{p^{*}}}\leq C_{p}\|f\|_{p},\quad p^{*}={\frac {np}{n-\alpha p}}.$

More generally, the operators I_α are well-defined for complex α such that 0 < Re α < n.

The Riesz potential can be defined more generally in a weak sense as the convolution

$I_{\alpha }f=f*K_{\alpha }\,$

where K_α is the locally integrable function:

$K_{\alpha }(x)={\frac {1}{c_{\alpha }}}{\frac {1}{|x|^{{n-\alpha }}}}.$

The Riesz potential can therefore be defined whenever f is a compactly supported distribution. In this connection, the Riesz potential of a positive Borel measure μ with compact support is chiefly of interest in potential theory because I_αμ is then a (continuous) subharmonic function off the support of μ, and is lower semicontinuous on all of Rⁿ.

Consideration of the Fourier transform reveals that the Riesz potential is a Fourier multiplier. In fact, one has

$\widehat {K_{\alpha }}(\xi )=|2\pi \xi |^{{-\alpha }}$

and so, by the convolution theorem,

$\widehat {I_{\alpha }f}(\xi )=|2\pi \xi |^{{-\alpha }}{\hat {f}}(\xi ).$

The Riesz potentials satisfy the following semigroup property on, for instance, rapidly decreasing continuous functions

$I_{\alpha }I_{\beta }=I_{{\alpha +\beta }}\$

provided

$0<\operatorname {Re\,}\alpha ,\operatorname {Re\,}\beta <n,\quad 0<\operatorname {Re\,}(\alpha +\beta )<n.$

Furthermore, if 2 < Re α <n, then

$\Delta I_{{\alpha +2}}=-I_{\alpha }.\$

One also has, for this class of functions,

$\lim _{{\alpha \to 0^{+}}}(I^{\alpha }f)(x)=f(x).$

References

Landkof, N. S. (1972), Foundations of modern potential theory, Berlin, New York: Springer-Verlag, MR 0350027
Riesz, Marcel (1949), "L'intégrale de Riemann-Liouville et le problème de Cauchy", Acta Mathematica 81: 1–223, doi:10.1007/BF02395016, ISSN 0001-5962, MR 0030102 .
Solomentsev, E.D. (2001), "Riesz potential", in Hazewinkel, Michiel, Encyclopedia of Mathematics, Springer, ISBN 978-1-55608-010-4
Stein, Elias (1970), Singular integrals and differentiability properties of functions, Princeton, NJ: Princeton University Press, ISBN 0-691-08079-8

This article is issued from Wikipedia. The text is available under the Creative Commons Attribution/Share Alike; additional terms may apply for the media files.

Riesz potential

See also

References