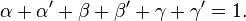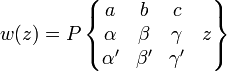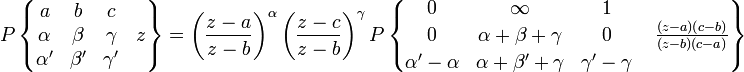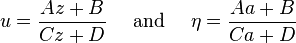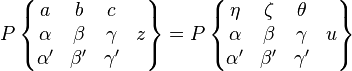Riemann's differential equation

From Wikipedia, the free encyclopedia

In mathematics, Riemann's differential equation, named after Bernhard Riemann, is a generalization of the hypergeometric differential equation, allowing the regular singular points to occur anywhere on the Riemann sphere, rather than merely at 0, 1, and ∞.

Definition

The differential equation is given by

{\frac {d^{2}w}{dz^{2}}}+\left[{\frac {1-\alpha -\alpha '}{z-a}}+{\frac {1-\beta -\beta '}{z-b}}+{\frac {1-\gamma -\gamma '}{z-c}}\right]{\frac {dw}{dz}}
+\left[{\frac {\alpha \alpha '(a-b)(a-c)}{z-a}}+{\frac {\beta \beta '(b-c)(b-a)}{z-b}}+{\frac {\gamma \gamma '(c-a)(c-b)}{z-c}}\right]{\frac {w}{(z-a)(z-b)(z-c)}}=0.

The regular singular points are a, b, and c. The pairs of exponents for each are respectively α; α′, β; β′, and γ; γ′. The exponents are subject to the condition

\alpha +\alpha '+\beta +\beta '+\gamma +\gamma '=1.

Solutions

The solutions are denoted by the Riemann P-symbol

w(z)=P\left\{{\begin{matrix}a&b&c&\;\\\alpha &\beta &\gamma &z\\\alpha '&\beta '&\gamma '&\;\end{matrix}}\right\}

The standard hypergeometric function may be expressed as

\;_{2}F_{1}(a,b;c;z)=P\left\{{\begin{matrix}0&\infty &1&\;\\0&a&0&z\\1-c&b&c-a-b&\;\end{matrix}}\right\}

The P-functions obey a number of identities; one of them allows a general P-function to be expressed in terms of the hypergeometric function. It is

P\left\{{\begin{matrix}a&b&c&\;\\\alpha &\beta &\gamma &z\\\alpha '&\beta '&\gamma '&\;\end{matrix}}\right\}=\left({\frac {z-a}{z-b}}\right)^{\alpha }\left({\frac {z-c}{z-b}}\right)^{\gamma }P\left\{{\begin{matrix}0&\infty &1&\;\\0&\alpha +\beta +\gamma &0&\;{\frac {(z-a)(c-b)}{(z-b)(c-a)}}\\\alpha '-\alpha &\alpha +\beta '+\gamma &\gamma '-\gamma &\;\end{matrix}}\right\}

In other words, one may write the solutions in terms of the hypergeometric function as

w(z)=\left({\frac {z-a}{z-b}}\right)^{\alpha }\left({\frac {z-c}{z-b}}\right)^{\gamma }\;_{2}F_{1}\left(\alpha +\beta +\gamma ,\alpha +\beta '+\gamma ;1+\alpha -\alpha ';{\frac {(z-a)(c-b)}{(z-b)(c-a)}}\right)

The full complement of Kummer's 24 solutions may be obtained in this way; see the article hypergeometric differential equation for a treatment of Kummer's solutions.

Fractional linear transformations

The P-function possesses a simple symmetry under the action of fractional linear transformations known as Möbius transformations (that are the conformal remappings of the Riemann sphere), or equivalently, under the action of the group GL(2, C). Given arbitrary complex numbers A, B, C, D such that AD − BC ≠ 0, define the quantities

u={\frac {Az+B}{Cz+D}}\quad {\text{ and }}\quad \eta ={\frac {Aa+B}{Ca+D}}

and

\zeta ={\frac {Ab+B}{Cb+D}}\quad {\text{ and }}\quad \theta ={\frac {Ac+B}{Cc+D}}

then one has the simple relation

P\left\{{\begin{matrix}a&b&c&\;\\\alpha &\beta &\gamma &z\\\alpha '&\beta '&\gamma '&\;\end{matrix}}\right\}=P\left\{{\begin{matrix}\eta &\zeta &\theta &\;\\\alpha &\beta &\gamma &u\\\alpha '&\beta '&\gamma '&\;\end{matrix}}\right\}

expressing the symmetry.

See also

References

This article is issued from Wikipedia. The text is available under the Creative Commons Attribution/Share Alike; additional terms may apply for the media files.