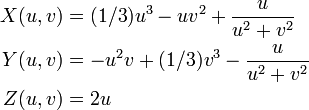Richmond surface

From Wikipedia, the free encyclopedia
Richmond surface for m=2.

In differential geometry, a Richmond surface is a minimal surface first described by Herbert William Richmond in 1904. [1] It is a family of surfaces with one planar end and one Enneper surface-like self-intersecting end.

It has Weierstrass–Enneper parameterization f(z)=1/z^{m},g(z)=z^{m}. This allows a parametrization based on a complex parameter as

{\begin{aligned}X(z)&=\Re [(-1/2z)-z^{{2m+1}}/(4m+2)]\\Y(z)&=\Re [(-i/2z)+iz^{{2m+1}}/(4m+2)]\\Z(z)&=\Re [z^{n}/n]\end{aligned}}

The associate family of the surface is just the surface rotated around the z-axis.

Taking m = 2 a real parametric expression becomes:[2]

{\begin{aligned}X(u,v)&=(1/3)u^{3}-uv^{2}+{\frac {u}{u^{2}+v^{2}}}\\Y(u,v)&=-u^{2}v+(1/3)v^{3}-{\frac {u}{u^{2}+v^{2}}}\\Z(u,v)&=2u\end{aligned}}

References

  1. ↑ Jesse Douglas, Tibor Radó, The Problem of Plateau: A Tribute to Jesse Douglas & Tibor Radó, World Scientific, 1992 (p. 239-240)
  2. ↑ John Oprea, The Mathematics of Soap Films: Explorations With Maple, American Mathematical Soc., 2000
This article is issued from Wikipedia. The text is available under the Creative Commons Attribution/Share Alike; additional terms may apply for the media files.