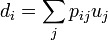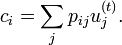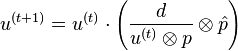Richardson–Lucy deconvolution

From Wikipedia, the free encyclopedia

Not to be confused with Modified Richardson iteration.

The Richardson–Lucy algorithm, also known as Lucy–Richardson deconvolution, is an iterative procedure for recovering a latent image that has been blurred by a known point spread function.^[1]^[2]

Pixels in the observed image can be represented in terms of the point spread function and the latent image as

$d_{{i}}=\sum _{{j}}p_{{ij}}u_{{j}}\,$

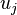where $p_{{ij}}$ is the point spread function (the fraction of light coming from true location $j$ that is observed at position $i$ ), $u_{{j}}$ is the pixel value at location $j$ in the latent image, and $d_{{i}}$ is the observed value at pixel location $i$ . The statistics are performed under the assumption that $u_{j}$ are Poisson distributed, which is appropriate for photon noise in the data.

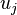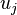The basic idea is to calculate the most likely $u_{j}$ given the observed $d_{i}$ and known $p_{{ij}}$ . This leads to an equation for $u_{j}$ which can be solved iteratively according to

$u_{{j}}^{{(t+1)}}=u_{j}^{{(t)}}\sum _{{i}}{\frac {d_{{i}}}{c_{{i}}}}p_{{ij}}$

where

$c_{{i}}=\sum _{{j}}p_{{ij}}u_{{j}}^{{(t)}}.$

It has been shown empirically that if this iteration converges, it converges to the maximum likelihood solution for 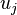$u_{j}$ .^[3]

This can also be written more generally (for more dimensions) in terms of convolution,^[4]

$u^{{(t+1)}}=u^{{(t)}}\cdot \left({\frac {d}{u^{{(t)}}\otimes p}}\otimes {\hat {p}}\right)$

where the division and multiplication are element wise, and ${\hat {p}}$ is the flipped point spread function, such that

${\hat {p}}_{{nm}}=p_{{(i-n)(j-m)}},0\leq n,m\leq i,j$

In problems where the point spread function $p_{{ij}}$ is dependent on one or more unknown parameters, the Richardson–Lucy algorithm cannot be used. A later and more general class of algorithms, the expectation-maximization algorithms,^[5] have been applied to this type of problem with great success

Implementation

For the two dimensional case this can be implemented in MATLAB, to estimate the latent greyscale image from a known blurred image and point spread function:

function latent_est = RL_deconvolution(observed, psf, iterations)
    % to utilise the conv2 function we must make sure the inputs are double
    observed = double(observed);
    psf      = double(psf);
    % initial estimate is arbitrary - uniform 50% grey works fine
    latent_est = 0.5*ones(size(observed));
    % create an inverse psf
    psf_hat = psf(end:-1:1,end:-1:1);
    % iterate towards ML estimate for the latent image
    for i= 1:iterations
        est_conv      = conv2(latent_est,psf,'same');
        relative_blur = observed./est_conv;
        error_est     = conv2(relative_blur,psf_hat,'same'); 
        latent_est    = latent_est.* error_est;
    end

The MATLAB image processing toolbox has an implementation in the function deconvlucy as well as a demo on its usage.

References

↑ Richardson, William Hadley (1972). "Bayesian-Based Iterative Method of Image Restoration". JOSA 62 (1): 55–59. doi:10.1364/JOSA.62.000055.
↑ Lucy, L. B. (1974). "An iterative technique for the rectification of observed distributions". Astronomical Journal 79 (6): 745–754. Bibcode:1974AJ.....79..745L. doi:10.1086/111605.
↑ Shepp, L. A.; Vardi, Y. (1982), "Maximum Likelihood Reconstruction for Emission Tomography", IEEE Transactions on Medical Imaging 1: 113, doi:10.1109/TMI.1982.4307558 Cite uses deprecated parameters (help)
↑ Fish D. A.,; Brinicombe A. M., Pike E. R., and Walker J. G. (1995), "Blind deconvolution by means of the Richardson–Lucy algorithm", Journal of the Optical Society of America A 12 (1): 58–65, Bibcode:1995JOSAA..12...58F, doi:10.1364/JOSAA.12.000058 Cite uses deprecated parameters (help)
↑ A.P. Dempster, N.M. Laird, D.B. Rubin, 1977, Maximum likelihood from incomplete data via the EM algorithm, J. Royal Stat. Soc. Ser. B, 39 (1), pp. 1–38

This article is issued from Wikipedia. The text is available under the Creative Commons Attribution/Share Alike; additional terms may apply for the media files.