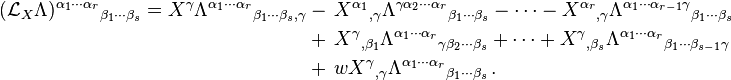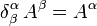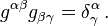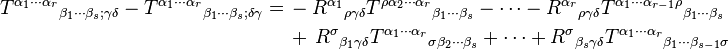Ricci calculus
In mathematics, Ricci calculus constitutes the rules of index notation and manipulation for tensors and tensor fields.[1][2][3] It is also the modern name for what used to be called the absolute differential calculus (the foundation of tensor calculus), developed by Gregorio Ricci-Curbastro in 1887–96, and subsequently popularized in a paper [4] written with his pupil Tullio Levi-Civita in 1900. Jan Arnoldus Schouten developed the modern notation and formalism for this mathematical framework, and made contributions to the theory, during its applications to general relativity and differential geometry in the early twentieth century.[5]
A component of a tensor is a real number which is used as a coefficient of a basis element for the tensor space. The tensor is the sum of its components multiplied by their basis elements. Tensors and tensor fields can be expressed in terms of their components, and operations on tensors and tensor fields can be expressed in terms of operations on their components. The description of tensor fields and operations on them in terms of their components is the focus of the Ricci calculus. This notation allows the most efficient expressions of such tensor fields and operations. While much of the notation may be applied with any tensors, operations relating to a differential structure are only applicable to tensor fields. Where needed, the notation extends to components of non-tensors, particularly multidimensional arrays.
A tensor may be expressed as a linear sum of the tensor product of vector and covector basis elements. The resulting tensor components are labelled by indices of the basis. Each index has one possible value per dimension of the underlying vector space. The number of indices equals the order of the tensor.
For compactness and convenience, the notational convention implies certain things, notably that of summation over indices repeated within a term and of universal quantification over free indices (those not so summed). Expressions in the notation of the Ricci calculus may generally be interpreted as a set of simultaneous equations relating the components as functions over a manifold, usually more specifically as functions of the coordinates on the manifold. This allows intuitive manipulation of expressions with familiarity of only a limited set of rules.
Notation for indices
Basis-related distinctions
Space–time split
Where a distinction is to be made between the space-like basis elements and a time-like element in the four dimensional spacetime of classical physics, this is conventionally done through indices as follows:[6]
- The lowercase Latin alphabet a, b, c... is used to indicate restriction to 3-dimensional Euclidean space, which take values 1, 2, 3 for the spatial components; and the time-like element, indicated by 0, is shown separately.
- The lowercase Greek alphabet α, β, γ... is used for 4-dimensional spacetime, which typically take values 0 for time components and 1, 2, 3 for the spatial components.
Some sources use 4 instead of 0 as the index value corresponding to time; in this article, 0 is used. Otherwise, in general mathematical contexts, any symbols can be used for the indices, generally running over all dimensions of the vector space.
Coordinate and index notation
The author(s) will usually make it clear whether a subscript is intended as an index or as a label.
For example, in 3-D Euclidean space and using Cartesian coordinates; the coordinate vector A = (A1, A2, A3) = (Ax, Ay, Az) shows a direct correspondence between the subscripts 1, 2, 3 and the labels x, y, z. In the expression Ai, i is interpreted as an index ranging over the values 1, 2, 3, while the x, y, z subscripts are not variable indices, more like "names" for the components. In the context of spacetime, the index value 0 corresponds to the label t.
Reference to coordinate systems
Indices themselves may be labelled using diacritic-like symbols, such as a hat (^), bar (–), tilde (~), or prime (′)
to denote a possibly different basis (and hence coordinate system) for that index. An example is in Lorentz transformations from one frame of reference to another, where one frame could be unprimed and the other primed, as in:
This is not to be confused with van der Waerden notation for spinors, which uses hats and overdots on indices to reflect the chiralty of a spinor.
Raised and lowered indices
A lower index (subscript) indicates covariance of the components with respect to that index: 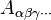
An upper index (superscript) indicates contravariance of the components with respect to that index: 
A tensor may have both upper and lower indices: 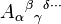
- Summation
Two indices (one raised and one lowered) with the same symbol within a term are summed over:  or
or 
The operation implied by such a summation is called tensor contraction:
More than one index may occur twice, but only twice within one term, for example:
As for a non-identity,
is not considered well-formed, that is, it is meaningless.
If a tensor has a list of indices all raised or lowered, one shorthand is to use a capital letter for the list:[7]
where I = i1 i2 ... in and J = j1 j2 ... jm.
- Sequential summation
Two vertical bars | | around a set of indices (with a contraction):[8]
denotes the summation in which each preceding index is counted up to (and not including) the value of the next index:
Only one group of the repeated set of indices has the vertical bars around them (the other contracted indices do not). More than one group can summed in this way:
where
This is useful to prevent over-counting in some summations, when tensors are symmetric or antisymmetric.
Alternatively, using the capital letter convention for multi-indices, an underarrow is placed underneath the block of indices:[9]
where
By contracting an index with a non-singular metric tensor, the type of a tensor can be changed, converting a lower index to an upper index or vice versa:
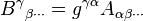 and
and 
The base symbol in many cases is retained (e.g. using A where B appears here), and when there is no ambiguity, repositioning an index may be taken to imply this operation.
Correlations between index positions and invariance
This table summarizes how the manipulation of covariant and contravariant indices fit in with invariance under a passive transformation between bases, with the components of each basis set in terms of the other reflected in the first column. The barred indices refer to the final coordinate system after the transformation.[10]
The Kronecker delta is used, see also below.
Basis transformation Component transformation Invariance Covector, covariant vector, dual vector, 1-form 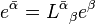
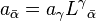
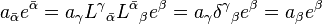
Vector, contravariant vector 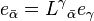

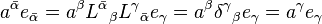
General outlines for index notation and operations
Tensors are equal if and only if every corresponding component is equal, e.g. tensor A equals tensor B if and only if
for all α, β and γ. Consequently, there are facets of the notation that are useful in checking that an equation makes sense (an analogous procedure to dimensional analysis).
- Free and dummy indices
Indices not in contractions are called free indices.
Indices in contractions are termed dummy indices, or summation indices.
- A tensor equation represents many ordinary (real-valued) equations
The components of tensors (like 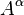 ,
,  etc.) are just real numbers. Since the indices take various integer values to select specific components of the tensors, a single tensor equation represents many ordinary equations. If a tensor equality has n free indices, and if the dimensionality of the underlying vector space is m, the equality represents mn equations: each has a specific set of index values.
etc.) are just real numbers. Since the indices take various integer values to select specific components of the tensors, a single tensor equation represents many ordinary equations. If a tensor equality has n free indices, and if the dimensionality of the underlying vector space is m, the equality represents mn equations: each has a specific set of index values.
For instance, if
is in 4-dimensions (that is, each index runs from 0 to 3 or 1 to 4), then because there are three free indices (α, β, δ), there are 43 = 64 equations. Three of these are:
This illustrates the compactness and efficiency of using index notation: many equations which all share a similar structure can be collected into one simple tensor equation.
- Indices are replaceable labels
Replacing any index symbol throughout by another leaves the tensor equation unchanged (provided there is no conflict with other symbols already used). This can be useful when manipulating indices, such as using index notation to verify vector calculus identities or identities of the Kronecker delta and Levi-Civita symbol (see also below). An example of a correct change is:
as for an erroneous change:
In the first replacement, λ replaced α and μ replaced γ everywhere, so the expression still has the same meaning. In the second, λ did not fully replace α, and μ did not fully replace γ (incidentally, the contraction on the γ index became a tensor product), which is entirely inconsistent for reasons shown next.
- Indices are the same in every term
The same indices on each side of a tensor equation always appear in the same (upper or lower) position throughout every term, except for indices repeated in a term (which implies a summation over that index), for example:
as for an erroneous expression:
In other words, non-repeated indices must be of the same type in every term of the equation. In the above identity α, β, δ line up throughout and γ occurs twice in one term due to a contraction (correctly once as an upper index and once as a lower index), so it's a valid as an expression. In the invalid expression, while β lines up, α and δ do not, and γ appears twice in one term (contraction) and once in another term, which is inconsistent.
- Brackets and punctuation used once where implied
When applying a rule to a number of indices (differentiation, symmetrization etc., shown next), the bracket or punctuation symbols denoting the rules are only shown on one group of the indices to which they apply.
If the brackets enclose covariant indices – the rule applies only to all covariant indices enclosed in the brackets, not to any contravariant indices which happen to be placed intermediately between the brackets.
Similarly if brackets enclose contravariant indices – the rule applies only to all enclosed contravariant indices, not to intermediately placed covariant indices.
Symmetric and antisymmetric parts
- Symmetric part of tensor
Parentheses ( ) around multiple indices denotes the symmetrized part of the tensor. When symmetrizing p indices using σ to range over permutations of the numbers 1 to p, one takes a sum over the permutations of those indices  for i = 1, 2, 3 ... p, and then divides by the number of permutations:
for i = 1, 2, 3 ... p, and then divides by the number of permutations:
For example, two symmetrizing indices mean there are two indices to permute and sum over:
while for three symmetrizing indices, there are three indices to sum over and permute:
The symmetrization is distributive over addition;
Indices are not part of the symmetrization when they are:
- not on the same level, for example;
- within the parentheses and between vertical bars (i.e. |···|), modifying the previous example;
Here the α and γ indices are symmetrized, β is not.
- Antisymmetric or alternating part of tensor
Square brackets [ ] around multiple indices denotes the antisymmetrized part of the tensor. For p antisymmetrizing indices – the sum over the permutations of those indices  multiplied by the signature of the permutation
multiplied by the signature of the permutation 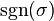 is taken, then divided by the number of permutations:
is taken, then divided by the number of permutations:
where n is the dimensionality of the underlying vector space and 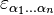 is the Levi-Civita symbol.
is the Levi-Civita symbol.
For example – two antisymmetrizing indices imply:
while three antisymmetrizing indices imply:
as for a more specific example, if F represents the electromagnetic tensor, then the equation
represents Gauss's law for magnetism and Faraday's law of induction.
As before, the antisymmetrization is distributive over addition;
As with symmetrization, indices are not antisymmetrized when they are:
- not on the same level, for example;
- within the square brackets and between vertical bars (i.e. |···|), modifying the previous example;
Here the α and γ indices are antisymmetrized, β is not.
- Symmetry and antisymmetry sum
Any tensor can be written as the sum of its symmetric and antisymmetric parts on two indices:
as can be seen by adding the above expressions for  and
and ![A_{{[\alpha \beta ]\gamma \cdots }}](/2014-wikipedia_en_all_02_2014/I/media/b/5/9/6/b5967f99b64b632808d06c5a14e732d6.png) . This does not hold for other than two indices.
. This does not hold for other than two indices.
Differentiation
For compactness, derivatives may be indicated by adding indices after a comma or semicolon.[11][12]
To indicate partial differentiation of a tensor field with respect to a coordinate variable  , a comma is placed before an added lower index of the coordinate variable.
, a comma is placed before an added lower index of the coordinate variable.
This may be repeated (without adding further commas):
These components do not transform covariantly. This derivative is characterized by the product rule and the derivatives of the coordinates
where δ is the Kronecker delta.
To indicate covariant differentiation of any tensor field, a semicolon ( ; ) is placed before an added lower (covariant) index. Less common alternatives to the semicolon include a forward slash ( / )[13] or in three-dimensional curved space just one vertical bar ( | ).[14]
For a contravariant vector: 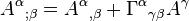 where
where 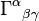 is a Christoffel symbol of the second kind.
is a Christoffel symbol of the second kind.
For a covariant vector: 
For an arbitrary tensor:[15]
The components of this derivative of a tensor field transform covariantly, and hence form another tensor field. This derivative is characterized by the product rule and the fact that the derivative of the metric 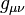 is zero:
is zero:
The covariant formulation of the directional derivative of any tensor field along a vector 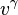 may be expressed as its contraction with the covariant derivative, e.g.:
may be expressed as its contraction with the covariant derivative, e.g.:
One alternative notation for the covariant derivative of any tensor is the subscripted nabla symbol  . For the case of a vector field
. For the case of a vector field 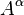 :[16]
:[16]
The Lie derivative is another derivative that is covariant, but which should not be confused with the covariant derivative. It is defined even in the absence of a metric. The Lie derivative of a type (r,s) tensor field  along (the flow of) a contravariant vector field
along (the flow of) a contravariant vector field 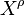 may be expressed as[17]
may be expressed as[17]
This derivative is characterized by the product rule and the fact that the derivative of the given contravariant vector field 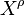 is zero.
is zero.
The Lie derivative of a type (r,s) relative tensor field  of weight
of weight 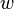 along (the flow of) a contravariant vector field
along (the flow of) a contravariant vector field 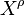 may be expressed as[18]
may be expressed as[18]
Notable tensors
The Kronecker delta is like the identity matrix
when multiplied and contracted. The components  are the same in any basis and form an invariant tensor of type (1,1), i.e. the identity of the tangent bundle over the identity mapping of the base manifold, and so its trace is an invariant.[19]
The dimensionality of spacetime is its trace:
are the same in any basis and form an invariant tensor of type (1,1), i.e. the identity of the tangent bundle over the identity mapping of the base manifold, and so its trace is an invariant.[19]
The dimensionality of spacetime is its trace:
in four-dimensional spacetime.
The metric tensor gives the length of any space-like curve
where y is any smooth strictly monotone parameterization of the path. It also gives the duration of any time-like curve
where t is any smooth strictly monotone parameterization of the trajectory. See also line element.
The inverse matrix (also indicated with a g) of the metric tensor is another important tensor
If this tensor is defined as
then it is the commutator of the covariant derivative with itself:[20][21]
since the connection 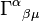 is torsionless, which means that the torsion tensor
is torsionless, which means that the torsion tensor  vanishes.
vanishes.
- Ricci identities
This can be generalized to get the commutator for two covariant derivatives of an arbitrary tensor as follows
which are often referred to as the Ricci identities.[22]
See also
- Regge calculus
- Tensor (intrinsic definition), Section: Basis
- Holonomic basis
- Exterior algebra
- Exterior calculus
- Differential form
- Hodge dual
- Penrose graphical notation
- Ricci decomposition
References
- ↑ Synge J.L., Schild A. (1949). Tensor Calculus. first Dover Publications 1978 edition. pp. 6–108.
- ↑ J.A. Wheeler, C. Misner, K.S. Thorne (1973). Gravitation. W.H. Freeman & Co. pp. 85–86, §3.5. ISBN 0-7167-0344-0.
- ↑ R. Penrose (2007). The Road to Reality. Vintage books. ISBN 0-679-77631-1.
- ↑ Ricci, Gregorio; Levi-Civita, Tullio (March 1900), "Méthodes de calcul différentiel absolu et leurs applications", Mathematische Annalen (Springer) 54 (1–2): 125–201, doi:10.1007/BF01454201
- ↑ Schouten, Jan A. (1924). R. Courant, ed. Der Ricci-Kalkül – Eine Einführung in die neueren Methoden und Probleme der mehrdimensionalen Differentialgeometrie (Ricci Calculus – An introduction in the latest methods and problems in multi-dimmensional differential geometry). Grundlehren der mathematischen Wissenschaften (in german) 10. Berlin: Springer Verlag.
- ↑ C. Møller (1952), The Theory of Relativity, p. 234 is an example of a variation: 'Greek indices run from 1 to 3, Latin indices from 1 to 4'
- ↑ T. Frankel (2012), The Geometry of Physics (3rd ed.), Cambridge University Press, p. 67, ISBN 978-1107-602601
- ↑ Gravitation, J.A. Wheeler, C. Misner, K.S. Thorne, W.H. Freeman & Co, 1973, ISBN 0-7167-0344-0
- ↑ T. Frankel (2012), The Geometry of Physics (3rd ed.), Cambridge University Press, p. 67, ISBN 978-1107-602601
- ↑ J.A. Wheeler, C. Misner, K.S. Thorne (1973). Gravitation. W.H. Freeman & Co. pp. 61, 202–203, 232. ISBN 0-7167-0344-0.
- ↑ G. Woan (2010). The Cambridge Handbook of Physics Formulas. Cambridge University Press. ISBN 978-0-521-57507-2.
- ↑ Covariant derivative – Mathworld, Wolfram
- ↑ T. Frankel (2012), The Geometry of Physics (3rd ed.), Cambridge University Press, p. 298, ISBN 978-1107-602601
- ↑ J.A. Wheeler, C. Misner, K.S. Thorne (1973). Gravitation. W.H. Freeman & Co. pp. 510, §21.5. ISBN 0-7167-0344-0.
- ↑ T. Frankel (2012), The Geometry of Physics (3rd ed.), Cambridge University Press, p. 299, ISBN 978-1107-602601
- ↑ D. McMahon (2006). Relativity. Demystified. McGraw Hill. p. 67. ISBN 0-07-145545-0.
- ↑ Bishop, R.L.; Goldberg, S.I. (1968), Tensor Analysis on Manifolds, p. 130
- ↑ Lovelock, David; Hanno Rund (1989). Tensors, Differential Forms, and Variational Principles. p. 123.
- ↑ Bishop, R.L.; Goldberg, S.I. (1968), Tensor Analysis on Manifolds, p. 85
- ↑ Synge J.L., Schild A. (1949). Tensor Calculus. first Dover Publications 1978 edition. pp. 83, p. 107.
- ↑ P. A. M. Dirac. General Theory of Relativity. pp. 20–21.
- ↑ Lovelock, David; Hanno Rund (1989). Tensors, Differential Forms, and Variational Principles. p. 84.
Books
- Bishop, R.L.; Goldberg, S.I. (1968), Tensor Analysis on Manifolds (First Dover 1980 ed.), The Macmillan Company, ISBN 0-486-64039-6
- Danielson, Donald A. (2003). Vectors and Tensors in Engineering and Physics (2/e ed.). Westview (Perseus). ISBN 978-0-8133-4080-7.
- Dimitrienko, Yuriy (2002). Tensor Analysis and Nonlinear Tensor Functions. Kluwer Academic Publishers (Springer). ISBN 1-4020-1015-X.
- Lovelock, David; Hanno Rund (1989) [1975]. Tensors, Differential Forms, and Variational Principles. Dover. ISBN 978-0-486-65840-7.
- C. Møller (1952), The Theory of Relativity (3rd ed.), Oxford University Press
- Synge J.L., Schild A. (1949). Tensor Calculus. first Dover Publications 1978 edition. ISBN 978-0-486-63612-2.
- J.R. Tyldesley (1975), An introduction to Tensor Analysis: For Engineers and Applied Scientists, Longman, ISBN 0-582-44355-5
- D.C. Kay (1988), Tensor Calculus, Schaum’s Outlines, McGraw Hill (USA), ISBN 0-07-033484-6
- T. Frankel (2012), The Geometry of Physics (3rd ed.), Cambridge University Press, ISBN 978-1107-602601
| ||||||||||||||||||||||||||||||||||||
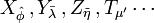
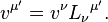
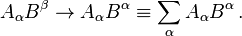



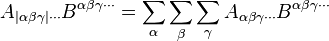
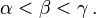

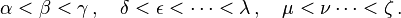
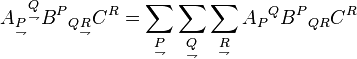
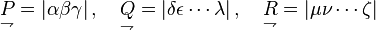
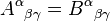

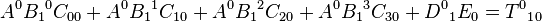
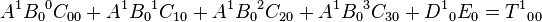

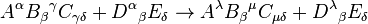



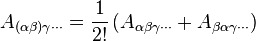




![{\begin{aligned}A_{{[\alpha _{1}\cdots \alpha _{p}]\alpha _{{p+1}}\cdots \alpha _{q}}}&={\dfrac {1}{p!}}\sum _{{\sigma }}\operatorname{sgn}(\sigma )A_{{\alpha _{{\sigma (1)}}\cdots \alpha _{{\sigma (p)}}\alpha _{{p+1}}\cdots \alpha _{{q}}}}\\&={\dfrac {1}{(n-p)!}}\varepsilon _{{\alpha _{1}\dots \alpha _{p}\,\beta _{1}\dots \beta _{{n-p}}}}{\dfrac {1}{p!}}\varepsilon ^{{\gamma _{1}\dots \gamma _{p}\,\beta _{1}\dots \beta _{{n-p}}}}A_{{\gamma _{1}\dots \gamma _{p}\alpha _{{p+1}}\cdots \alpha _{q}}}\\\end{aligned}}](/2014-wikipedia_en_all_02_2014/I/media/e/5/5/9/e55909cf3446550150f835bae50718e3.png)
![A_{{[\alpha \beta ]\gamma \cdots }}={\dfrac {1}{2!}}\left(A_{{\alpha \beta \gamma \cdots }}-A_{{\beta \alpha \gamma \cdots }}\right)](/2014-wikipedia_en_all_02_2014/I/media/b/f/7/c/bf7cf0423101005a6376cbf3ed8dbf5a.png)
![A_{{[\alpha \beta \gamma ]\delta \cdots }}={\dfrac {1}{3!}}\left(A_{{\alpha \beta \gamma \delta \cdots }}+A_{{\gamma \alpha \beta \delta \cdots }}+A_{{\beta \gamma \alpha \delta \cdots }}-A_{{\alpha \gamma \beta \delta \cdots }}-A_{{\gamma \beta \alpha \delta \cdots }}-A_{{\beta \alpha \gamma \delta \cdots }}\right)](/2014-wikipedia_en_all_02_2014/I/media/1/9/f/8/19f8dd33d3d017c5d5879384c750200f.png)
![0=F_{{[\alpha \beta ,\gamma ]}}={\dfrac {1}{3!}}\left(F_{{\alpha \beta ,\gamma }}+F_{{\gamma \alpha ,\beta }}+F_{{\beta \gamma ,\alpha }}-F_{{\beta \alpha ,\gamma }}-F_{{\alpha \gamma ,\beta }}-F_{{\gamma \beta ,\alpha }}\right)\,](/2014-wikipedia_en_all_02_2014/I/media/6/2/5/0/6250a45e1e1e025701f30e830d3d6038.png)
![A_{{[\alpha }}\left(B_{{\beta ]\gamma \cdots }}+C_{{\beta ]\gamma \cdots }}\right)=A_{{[\alpha }}B_{{\beta ]\gamma \cdots }}+A_{{[\alpha }}C_{{\beta ]\gamma \cdots }}](/2014-wikipedia_en_all_02_2014/I/media/6/5/4/3/654301a98f35c15cf1e6137f127df860.png)
![A_{{[\alpha }}B^{{\beta }}{}_{{\gamma ]}}={\dfrac {1}{2!}}\left(A_{{\alpha }}B^{{\beta }}{}_{{\gamma }}-A_{{\gamma }}B^{{\beta }}{}_{{\alpha }}\right)](/2014-wikipedia_en_all_02_2014/I/media/0/8/5/4/085445c660af1f84f55cec0b1bf2184d.png)
![A_{{[\alpha }}B_{{|\beta |}}{}_{{\gamma ]}}={\dfrac {1}{2!}}\left(A_{{\alpha }}B_{{\beta \gamma }}-A_{{\gamma }}B_{{\beta \alpha }}\right)](/2014-wikipedia_en_all_02_2014/I/media/c/3/9/d/c39d967f4aebb0d0e2f98b273fc73ad3.png)
![A_{{\alpha \beta \gamma \cdots }}=A_{{(\alpha \beta )\gamma \cdots }}+A_{{[\alpha \beta ]\gamma \cdots }}](/2014-wikipedia_en_all_02_2014/I/media/6/3/2/5/63250c622dcf6aca1662283fd25eb038.png)


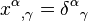
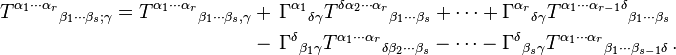


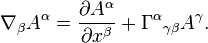

![({\mathcal {L}}_{X}X)^{{\rho }}=[X,X]^{{\rho }}=0\,.](/2014-wikipedia_en_all_02_2014/I/media/7/9/a/f/79af8d21236a61f0871150b9af7d918b.png)