Rhombohedron

Rhombohedron
Type	Prism
Faces	6 rhombi
Edges	12
Vertices	8
Symmetry group	Ci, [2+,2+], (×), order 2
Properties	convex, zonohedron

In geometry, a rhombohedron is a three-dimensional figure like a cube, except that its faces are not squares but rhombi. It is a special case of a parallelepiped where all edges are the same length. It can be used to define the rhombohedral lattice system, a honeycomb with rhombohedral cells.

In general the rhombohedron can have three types of rhombic faces in congruent opposite pairs, C_i symmetry, order 2.

Four points forming non-adjacent vertices of a rhombohedron necessarily form the four vertices of an orthocentric tetrahedron, and all orthocentric tetrahedra can be formed in this way.^[1]

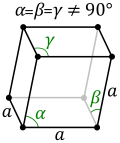
Rhombohedral lattice system

The rhombohedral lattice system has rhombohedral cells, with 3 pairs of unique rhombic faces:

Special cases

• Cube: with O_h symmetry, order 48. All faces are squares.
• Trigonal trapezohedron: with D_3d symmetry, order 12. If all of the non-obtuse internal angles of the faces are equal (all faces are same). This can be see by stretching a cube on its body-digonal axis. For example a regular octahedron with two tetrahedra attached on opposite faces constructs a 60 degree trigonal trapezohedron:
• Right rhombic prism: with D_2h symmetry, order 8. It constructed by two rhombi and 4 squares. This can be see by stretching a cube on its face-digonal axis. For example two triangular prisms attached together makes a 60 degree rhombic prism.
• A general rhombic prism: With C_2h symmetry, order 4. It has only one plane of symmetry through four vertices, and 6 rhombic faces.

References

External links

• Weisstein, Eric W., "Rhombohedron", MathWorld.
• "golden" rhombohedron
• "silver" rhombohedron