Rhombitrihexagonal tiling
| Rhombitrihexagonal tiling | |
|---|---|
 | |
| Type | Semiregular tiling |
| Vertex configuration | 3.4.6.4 |
| Schläfli symbol | rr{6,3} |
| Wythoff symbol | 3 | 6 2 |
| Coxeter diagram |     |
| Symmetry | p6m, [6,3], (*632) |
| Rotation symmetry | p6, [6,3]+, (632) |
| Bowers acronym | Rothat |
| Dual | Deltoidal trihexagonal tiling |
| Properties | Vertex-transitive |
 Vertex figure: 3.4.6.4 | |
In geometry, the rhombitrihexagonal tiling is a semiregular tiling of the Euclidean plane. There are one triangle, two squares, and one hexagon on each vertex. It has Schläfli symbol of rr{3,6}.
John Conway calls it a rhombihexadeltille.[1] It can be considered a cantellated by Norman Johnson's terminology or an expanded hexagonal tiling by Alicia Boole Stott's operational language.
There are 3 regular and 8 semiregular tilings in the plane.
Uniform colorings
There is only one uniform coloring in a rhombitrihexagonal tiling. (Naming the colors by indices around a vertex (3.4.6.4): 1232.)
With edge-colorings there is a half symmetry form (3*3) orbifold notation. The hexagons can be considered as truncated triangles, t{3} with two types of edges. It has Coxeter diagram 
, Schläfli symbol s2{3,6}. The bicolored square can be distorted into isosceles trapezoids. In the limit, where the rectangles degenerate into edges, a triangular tiling results, constructed as a snub triangular tiling, .
| Symmetry | [6,3], (*632) | [6,3+], (3*3) | |
|---|---|---|---|
| Name | Rhombitrihexagonal tiling | Cantic snub triangular tiling | Snub triangular tiling |
| Image |  Uniform face coloring |
 Uniform edge coloring |
 Snub triangular tiling |
| Schläfli symbol Coxeter diagram |
rr{3,6} |
s2{3,6} |
s{3,6} |
Related polyhedra and tilings
There are eight uniform tilings that can be based from the regular hexagonal tiling (or the dual triangular tiling). Drawing the tiles colored as red on the original faces, yellow at the original vertices, and blue along the original edges, there are 8 forms, 7 which are topologically distinct. (The truncated triangular tiling is topologically identical to the hexagonal tiling.)
| Symmetry: [6,3], (*632) | [6,3]+ (632) |
[1+,6,3] (*333) |
[6,3+] (3*3) | |||||||
|---|---|---|---|---|---|---|---|---|---|---|
| {6,3} | t{6,3} | r{6,3} r{3[3]} |
t{3,6} t{3[3]} |
{3,6} {3[3]} |
rr{6,3} s2{6,3} |
tr{6,3} | sr{6,3} | h{6,3} {3[3]} |
h2{6,3} r{3[3]} |
s{3,6} s{3[3]} |
|
|
|
|
|
|
|
|
| ||
 =   |
= |
=  |
|
 = or  |
= or |
=  | ||||
 |
 |
  |
  |
  |
 |
 |
 |
  |
  |
  |
| Uniform duals | ||||||||||
| V63 | V3.122 | V(3.6)2 | V63 | V36 | V3.4.12.4 | V.4.6.12 | V34.6 | V36 | V(3.6)2 | V36 |
 |
|
|
|
|
|
|
 |
|
|
|
|
 |
 |
|
|
 |
 |
 |
|
|
|
This tiling is topologically related as a part of sequence of cantellated polyhedra with vertex figure (3.4.n.4), and continues as tilings of the hyperbolic plane. These vertex-transitive figures have (*n32) reflectional symmetry.
| Symmetry *n32 [n,3] |
Spherical | Euclidean | Hyperbolic... | |||||
|---|---|---|---|---|---|---|---|---|
| *232 [2,3] D3h |
*332 [3,3] Td |
*432 [4,3] Oh |
*532 [5,3] Ih |
*632 [6,3] P6m |
*732 [7,3] |
*832 [8,3]... |
*∞32 [∞,3] | |
| Expanded figure |
 3.4.2.4 |
 3.4.3.4 |
 3.4.4.4 |
 3.4.5.4 |
 3.4.6.4 |
 3.4.7.4 |
 3.4.8.4 |
 3.4.∞.4 |
| Coxeter Schläfli |
 rr{2,3} |
rr{3,3} |
 rr{4,3} |
 rr{5,3} |
rr{6,3} |
 rr{7,3} |
 rr{8,3} |
 rr{∞,3} |
| Deltoidal figure | 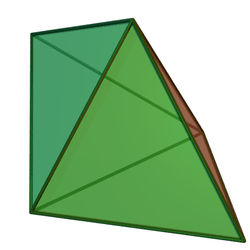 V3.4.2.4 |
 V3.4.3.4 |
 V3.4.4.4 |
 V3.4.5.4 |
V3.4.6.4 |
 V3.4.7.4 |
 V3.4.8.4 |
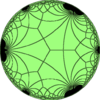 V3.4.∞.4 |
| Coxeter | |
|
|
|
|
|
|
|
The hexagonal cupola contains the pattern of this tiling, but closes it into a degenerate polygon with a dodecagon base.
| 2 | 3 | 4 | 5 | 6 |
|---|---|---|---|---|
 Digonal cupola |
 Triangular cupola |
 Square cupola |
 Pentagonal cupola |
 Hexagonal cupola (Flat) |
Circle packing
The Rhombitrihexagonal tiling can be used as a circle packing, placing equal diameter circles at the center of every point. Every circle is in contact with 4 other circles in the packing (kissing number). The gap inside each hexagon allows for one circle, for a denser packing with kissing number 5.
Gallery
 An ornamental version |
 Nonuniform pattern (with rectangles) |
 The game Kensington |
See also
 |
Wikimedia Commons has media related to Uniform tiling 3-4-6-4. |
- Tilings of regular polygons
- List of uniform tilings
Notes
- ↑ Conway, 2008, p288 table
References
- Grünbaum, Branko ; and Shephard, G. C. (1987). Tilings and Patterns. New York: W. H. Freeman. ISBN 0-7167-1193-1. (Chapter 2.1: Regular and uniform tilings, p. 58-65)
- Williams, Robert (1979). The Geometrical Foundation of Natural Structure: A Source Book of Design. Dover Publications, Inc. ISBN 0-486-23729-X. p40
- John H. Conway, Heidi Burgiel, Chaim Goodman-Strass, The Symmetries of Things 2008, ISBN 978-1-56881-220-5 (Chapter 21, Naming Archimedean and Catalan polyhedra and tilings.
- Weisstein, Eric W., "Uniform tessellation", MathWorld.
- Weisstein, Eric W., "Semiregular tessellation", MathWorld.
- Richard Klitzing, 2D Euclidean tilings, x3o6x - rothat - O8