Rhombitriapeirogonal tiling
| Rhombitriapeirogonal tiling | |
|---|---|
 Poincaré disk model of the hyperbolic plane | |
| Type | Hyperbolic uniform tiling |
| Vertex figure | 3.4.∞.4 |
| Schläfli symbol | rr{∞,3} s2{3,∞} |
| Wythoff symbol | 3 | ∞ 2 |
| Coxeter diagram |      |
| Symmetry group | [∞,3], (*∞32) [∞,3+], (3*∞) |
| Dual | Deltoidal triapeirogonal tiling |
| Properties | Vertex-transitive |
In geometry, the rhombtriapeirogonal tiling is a uniform tiling of the hyperbolic plane with a Schläfli symbol of rr{∞,3}.
Symmetry
This tiling has [∞,3], (*∞32) symmetry. There is only one uniform coloring.
Similar to the Euclidean rhombitrihexagonal tiling, by edge-coloring there is a half symmetry form (3*∞) orbifold notation. The apeireogons can be considered as truncated, t{∞} with two types of edges. It has Coxeter diagram , Schläfli symbol s2{3,∞}. The squares can be distorted into isosceles trapezoids. In the limit, where the rectangles degenerate into edges, an infinite-order triangular tiling results, constructed as an snub triapeirotrigonal tiling, .
Related polyhedra and tiling
This hyperbolic tiling is topologically related as a part of sequence of uniform cantellated polyhedra with vertex configurations (3.4.n.4), and [n,3] Coxeter group symmetry.
| Symmetry *n32 [n,3] |
Spherical | Euclidean | Hyperbolic... | |||||
|---|---|---|---|---|---|---|---|---|
| *232 [2,3] D3h |
*332 [3,3] Td |
*432 [4,3] Oh |
*532 [5,3] Ih |
*632 [6,3] P6m |
*732 [7,3] |
*832 [8,3]... |
*∞32 [∞,3] | |
| Expanded figure |
 3.4.2.4 |
 3.4.3.4 |
 3.4.4.4 |
 3.4.5.4 |
 3.4.6.4 |
 3.4.7.4 |
 3.4.8.4 |
3.4.∞.4 |
| Coxeter Schläfli |
 rr{2,3} |
rr{3,3} |
 rr{4,3} |
 rr{5,3} |
 rr{6,3} |
 rr{7,3} |
 rr{8,3} |
rr{∞,3} |
| Deltoidal figure |  V3.4.2.4 |
 V3.4.3.4 |
 V3.4.4.4 |
 V3.4.5.4 |
 V3.4.6.4 |
 V3.4.7.4 |
 V3.4.8.4 |
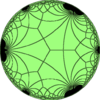 V3.4.∞.4 |
| Coxeter |  |
|
|
|
|
|
|
|
| Symmetry: [∞,3], (*∞32) | [∞,3]+ (∞32) |
[1+,∞,3] (*∞33) |
[∞,3+] (3*∞) | |||||||
|---|---|---|---|---|---|---|---|---|---|---|
|
|
|
|
|
|
|
|
 |
| |
 |
 |
 |
 |
 |
|
 |
 |
 |
||
| {∞,3} | t{∞,3} | r{∞,3} | t{3,∞} | {3,∞} | rr{∞,3} | tr{∞,3} | sr{∞,3} | h{∞,3} | s{3,∞} | |
| Uniform duals | ||||||||||
|
|
|
|
|
|
|
 |
|
| |
|
 |
 |
 |
|
|
 |
||||
| V∞3 | V3.∞.∞ | V(3.∞)2 | V6.6.∞ | V3∞ | V4.3.4.∞ | V4.6.∞ | V3.3.3.3.∞ | V(3.∞)3 | V3.3.3.3.3.∞ | |
See also
 |
Wikimedia Commons has media related to Uniform tiling 3-4-i-4. |
- List of uniform planar tilings
- Tilings of regular polygons
- Uniform tilings in hyperbolic plane
References
- John H. Conway, Heidi Burgiel, Chaim Goodman-Strass, The Symmetries of Things 2008, ISBN 978-1-56881-220-5 (Chapter 19, The Hyperbolic Archimedean Tessellations)
- "Chapter 10: Regular honeycombs in hyperbolic space". The Beauty of Geometry: Twelve Essays. Dover Publications. 1999. ISBN 0-486-40919-8. LCCN 99035678.