Rho meson
In particle physics, a rho meson is a short-lived hadronic particle that is an isospin triplet whose three states are denoted as ρ+, ρ0 and ρ−. After the pions and kaons, the rho mesons are the lightest strongly interacting particle with a mass of roughly 770 MeV for all three states. There should be a small mass difference between the ρ+ and the ρ0 that can be attributed to the electromagnetic self-energy of the particle as well as a small effect due to isospin breaking arising from the light quark masses; however, the current experimental limit is that this mass difference is less than 0.7 MeV.
The rho mesons have a very short lifetime and their decay width is about 145 MeV with the peculiar feature that the decay widths are not described by a Breit-Wigner form. The principal decay route of the rho mesons is to a pair of pions with a branching rate of 99.9%. Neutral rho mesons can decay to a pair of electrons or muons which occurs with a branching ratio of 5×10−5. This decay of the neutral rho to leptons can be interpreted as a mixing between the photon and rho. In principle the charged rho mesons mix with the weak vector bosons and can lead to decay to an electron or muon plus a neutrino; however, this has never been observed.
In the De Rujula–Georgi–Glashow description of hadrons,[1] the rho mesons can be interpreted as a bound state of a quark and an anti-quark and is an excited version of the pion. Unlike the pion, the rho meson has spin j = 1 (a vector meson) and a much higher value of the mass. This mass difference between the pions and rho mesons is attributed to a large hyperfine interaction between the quark and anti-quark. The main objection with the De Rujula–Georgi–Glashow description is that it attributes the lightness of the pions as an accident rather than a result of chiral symmetry breaking.
The rho mesons can be thought of as the gauge bosons of a spontaneously broken gauge symmetry whose local character is emergent (arising from QCD); Note that this broken gauge symmetry (sometimes called hidden local symmetry) is distinct from the global chiral symmetry acting on the flavors. This was described by Howard Georgi in a paper titled "The Vector Limit of Chiral Symmetry" where he ascribed much of the literature of hidden local symmetry to a non-linear sigma model.[2]
More recently, the point of view that the rho mesons are gauge bosons has been enhanced by a program known as AdS/QCD, which is an application of AdS/CFT derived from string theory. In this description, there is a small extra dimension that is a slice of anti-de Sitter space. The global flavor symmetries are promoted to five dimensional gauge symmetries that are broken at the boundary between space and isospin. The rho mesons are lightest Kaluza–Klein resonances of the fifth dimension. This program has the advantage that it is capable of making quantitative predictions for the interactions of the rho mesons. These predictions are usually accurate to 10%. There is some concern as to whether this five dimensional description is under perturbative control and this is currently under active research. Conceptually, the AdS/QCD approach is very close in spirit to "The Vector Limit of Chiral Symmetry"; if one deconstructs the 5th dimension, one finds an effective field theory very similar to the one described in the "Vector Limit."
| Particle name | Particle symbol |
Antiparticle symbol |
Quark content[3] |
Rest mass (MeV/c2) | IG | JPC | S | C | B' | Mean lifetime (s) | Commonly decays to (>5% of decays) |
|---|---|---|---|---|---|---|---|---|---|---|---|
| Charged rho meson[4] | ρ+(770) | ρ−(770) | ud | 775.4±0.4 | 1+ | 1− | 0 | 0 | 0 | ~4.5×10−24[a][b] | π± + π0 |
| Neutral rho meson[4] | ρ0(770) | Self | 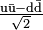 |
775.49±0.34 | 1+ | 1−− | 0 | 0 | 0 | ~4.5×10−24[a][b] | π+ + π− |
[a] ^ PDG reports the resonance width (Γ). Here the conversion τ = ħ⁄Γ is given instead.
[b] ^ The exact value depends on the method used. See the given reference for detail.
References
- ↑ Rujula, Georgi, Glashow (1975) "Hadron Masses in Gauge Theory." Physical Review D12, p.147
- ↑ H. Georgi. (1990) "Vector Realization of Chiral Symmetry." inSPIRE Record
- ↑ C. Amsler et al. (2008): Quark Model
- ↑ 4.0 4.1 C. Amsler et al. (2008): Particle listings – ρ
| ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||