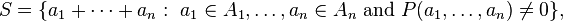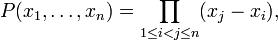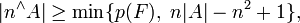Restricted sumset
In additive number theory and combinatorics, a restricted sumset has the form
where  are finite nonempty subsets of a field F and
are finite nonempty subsets of a field F and 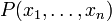 is a polynomial over F.
is a polynomial over F.
When 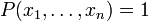 , S is the usual sumset
, S is the usual sumset  which is denoted by nA if
which is denoted by nA if  ; when
; when
S is written as  which is denoted by
which is denoted by  if
if  . Note that |S| > 0 if and only if there exist
. Note that |S| > 0 if and only if there exist 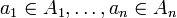 with
with  .
.
Cauchy–Davenport theorem
The Cauchy–Davenport theorem named after Augustin Louis Cauchy and Harold Davenport asserts that for any prime p and nonempty subsets A and B of the prime order cyclic group Z/pZ we have the inequality[1][2]
We may use this to deduce the Erdős-Ginzburg-Ziv theorem: given any 2n−1 elements of Z/n, there is a non-trivial subset that sums to zero modulo n. (Here n does not need to be prime.)[3][4]
A direct consequence of the Cauchy-Davenport theorem is: Given any set S of p−1 or more elements, not necessarily distinct, of Z/pZ, every element of Z/pZ can be written as the sum of the elements of some subset (possibly empty) of S.[5]
Kneser's theorem generalises this to finite abelian groups.[6]
Erdős–Heilbronn conjecture
The Erdős–Heilbronn conjecture posed by Paul Erdős and Hans Heilbronn in 1964 states that  if p is a prime and A is a nonempty subset of the field Z/pZ.[7] This was first confirmed by J. A. Dias da Silva and Y. O. Hamidoune in 1994[8]
who showed that
if p is a prime and A is a nonempty subset of the field Z/pZ.[7] This was first confirmed by J. A. Dias da Silva and Y. O. Hamidoune in 1994[8]
who showed that
where A is a finite nonempty subset of a field F, and p(F) is a prime p if F is of characteristic p, and p(F) = ∞ if F is of characteristic 0. Various extensions of this result were given by Noga Alon, M. B. Nathanson and I. Ruzsa in 1996,[9] Q. H. Hou and Zhi-Wei Sun in 2002,[10] and G. Karolyi in 2004.[11]
Combinatorial Nullstellensatz
A powerful tool in the study of lower bounds for cardinalities of various restricted sumsets is the following fundamental principle: the combinatorial Nullstellensatz.[12] Let  be a polynomial over a field F. Suppose that the coefficient of the monomial
be a polynomial over a field F. Suppose that the coefficient of the monomial 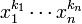 in
in  is nonzero and
is nonzero and 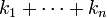 is the total degree of
is the total degree of  . If
. If  are finite subsets of F with
are finite subsets of F with 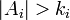 for
for  , then there are
, then there are 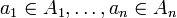 such that
such that  .
.
The method using the combinatorial Nullstellensatz is also called the polynomial method. This tool was rooted in a paper of N. Alon and M. Tarsi in 1989,[13] and developed by Alon, Nathanson and Ruzsa in 1995-1996,[9] and reformulated by Alon in 1999.[12]
References
- ↑ Nathanson (1996) p.44
- ↑ Geroldinger & Ruzsa (2009) pp.141–142
- ↑ Nathanson (1996) p.48
- ↑ Geroldinger & Ruzsa (2009) p.53
- ↑ Wolfram's MathWorld, Cauchy-Davenport Theorem, http://mathworld.wolfram.com/Cauchy-DavenportTheorem.html, accessed 20 June 2012.
- ↑ Geroldinger & Ruzsa (2009) p.143
- ↑ Nathanson (1996) p.77
- ↑ Dias da Silva, J. A.; Hamidoune, Y. O. (1994). "Cyclic spaces for Grassman derivatives and additive theory". Bulletin of the London Mathematical Society 26 (2): 140–146. doi:10.1112/blms/26.2.140.
- ↑ 9.0 9.1 Alon, Noga; Nathanson, Melvyn B.; Ruzsa, Imre (1996). "The polynomial method and restricted sums of congruence classes". Journal of Number Theory 56 (2): 404–417. doi:10.1006/jnth.1996.0029. MR 1373563.
- ↑ Hou, Qing-Hu; Sun, Zhi-Wei (2002). "Restricted sums in a field". Acta Arithmetica 102 (3): 239–249. doi:10.4064/aa102-3-3. MR 1884717.
- ↑ Károlyi, Gyula (2004). "The Erdős–Heilbronn problem in abelian groups". Israel Journal of Mathematics 139: 349–359. doi:10.1007/BF02787556. MR 2041798.
- ↑ 12.0 12.1 Alon, Noga (1999). "Combinatorial Nullstellensatz". Combinatorics, Probability and Computing 8 (1–2): 7–29. doi:10.1017/S0963548398003411. MR 1684621.
- ↑ Alon, Noga; Tarsi, Michael (1989). "A nowhere-zero point in linear mappings". Combinatorica 9 (4): 393–395. doi:10.1007/BF02125351. MR 1054015.
- Geroldinger, Alfred; Ruzsa, Imre Z., eds. (2009). Combinatorial number theory and additive group theory. Advanced Courses in Mathematics CRM Barcelona. Elsholtz, C.; Freiman, G.; Hamidoune, Y. O.; Hegyvári, N.; Károlyi, G.; Nathanson, M.; Solymosi, J.; Stanchescu, Y. With a foreword by Javier Cilleruelo, Marc Noy and Oriol Serra (Coordinators of the DocCourse). Basel: Birkhäuser. ISBN 978-3-7643-8961-1. Zbl 1177.11005.
- Nathanson, Melvyn B. (1996). Additive Number Theory: Inverse Problems and the Geometry of Sumsets. Graduate Texts in Mathematics 165. Springer-Verlag. ISBN 0-387-94655-1. Zbl 0859.11003.
External links
- Sun, Zhi-Wei (2006). "An additive theorem and restricted sumsets". Math. Res. Lett. , no. 15 (6): 1263–1276. arXiv:math.CO/0610981.
- Zhi-Wei Sun: On some conjectures of Erdős-Heilbronn, Lev and Snevily (PDF), a survey talk.
- Weisstein, Eric W., "Erdos-Heilbronn Conjecture", MathWorld.