Restricted Lie algebra
In mathematics, a restricted Lie algebra is a Lie algebra together with an additional "p operation."
Definition
Let L be a Lie algebra over a field k of characteristic p>0. A p operation on L is a map ![X\mapsto X^{{[p]}}](/2014-wikipedia_en_all_02_2014/I/media/e/3/0/1/e301165808c955cb1d407d487f2c9fbe.png) satisfying
satisfying
-
![{\mathrm {ad}}(X^{{[p]}})={\mathrm {ad}}(X)^{p}](/2014-wikipedia_en_all_02_2014/I/media/c/0/a/6/c0a6ef8253f4957fa1f76433a899cb4f.png) for all
for all 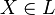 ,
, -
![(tX)^{{[p]}}=t^{p}X^{{[p]}}](/2014-wikipedia_en_all_02_2014/I/media/2/c/2/4/2c2485614bcd1288254834d00e4450c3.png) for all
for all  ,
, -
![(X+Y)^{{[p]}}=X^{{[p]}}+Y^{{[p]}}+\sum _{{i=1}}^{{p-1}}{\frac {s_{i}(X,Y)}{i}}](/2014-wikipedia_en_all_02_2014/I/media/4/6/1/c/461cb27a9941f90aae1b645e8c6be6b8.png) , for all
, for all 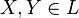 , where
, where 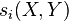 is the coefficient of
is the coefficient of  in the formal expression
in the formal expression  .
.
If the characteristic of k is 0, then L is a restricted Lie algebra where the p operation is the identity map.
Examples
For any associative algebra A defined over a field of characteristic p, the bracket operation ![[X,Y]:=XY-YX](/2014-wikipedia_en_all_02_2014/I/media/9/7/3/0/973030c31d130c5fe5f1f98e7d1b4dc8.png) and p operation
and p operation ![X^{{[p]}}:=X^{p}](/2014-wikipedia_en_all_02_2014/I/media/d/0/a/2/d0a2a5564d568e4432cca5a8ccb4a859.png) make A into a restricted Lie algebra
make A into a restricted Lie algebra 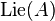 .
.
Let G be an algebraic group over a field k of characteristic p, and 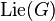 be the Zariski tangent space at the identity element of G. Each element of
be the Zariski tangent space at the identity element of G. Each element of 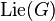 uniquely defines a left-invariant vector field on G, and the commutator of vector fields defines a Lie algebra structure on
uniquely defines a left-invariant vector field on G, and the commutator of vector fields defines a Lie algebra structure on 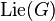 just as in the Lie group case. If p>0, the Frobenius map
just as in the Lie group case. If p>0, the Frobenius map 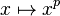 defines a p operation on
defines a p operation on 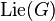 .
.
Restricted universal enveloping algebra
The functor 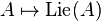 has a left adjoint
has a left adjoint ![L\mapsto U^{{[p]}}(L)](/2014-wikipedia_en_all_02_2014/I/media/e/1/4/a/e14a023839b695276b024337060cbbb0.png) called the restricted universal enveloping algebra. To construct this, let
called the restricted universal enveloping algebra. To construct this, let 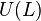 be the universal enveloping algebra of L forgetting the p operation. Letting I be the two-sided ideal generated by elements of the form
be the universal enveloping algebra of L forgetting the p operation. Letting I be the two-sided ideal generated by elements of the form ![x^{p}-x^{{[p]}}](/2014-wikipedia_en_all_02_2014/I/media/1/1/e/e/11eee8512caa738354514d13868c559b.png) , we set
, we set ![U^{{[p]}}(L)=U(L)/I](/2014-wikipedia_en_all_02_2014/I/media/c/b/2/1/cb212346f429e7f8ae96208c1a8b85bd.png) .
.
See also
Restricted Lie algebras are used in Jacobson's Galois correspondence for purely inseparable extensions of fields of exponent 1.
References
- Armand Borel, Linear Algebraic Groups 2nd edition, Graduate Texts in Mathematics 126, Springer-Verlag.
- Block, Richard E.; Wilson, Robert Lee (1988), "Classification of the restricted simple Lie algebras", Journal of Algebra 114 (1): 115–259, doi:10.1016/0021-8693(88)90216-5, ISSN 0021-8693, MR 931904