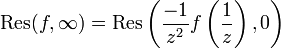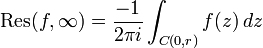Residue at infinity

From Wikipedia, the free encyclopedia

In complex analysis a branch of mathematics, the residue at infinity is a residue of a holomorphic function on an annulus having an infinite external radius. The infinity \infty is a point added to the local space {\mathbb C} in order to render it compact (in this case it is a one-point compactification). This space noted {\hat {{\mathbb C}}} is isomorphic to the Riemann sphere.[1] One can use the residue at infinity to calculate some integrals.

Definition

Given a holomorphic function f on an annulus 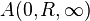A(0,R,\infty ) (centered at 0, with inner radius R and infinite outer radius), the residue at infinity of the function f can be defined in terms of the usual residue as follows:

{\mathrm {Res}}(f,\infty )={\mathrm {Res}}\left({-1 \over z^{2}}f\left({1 \over z}\right),0\right)

Thus, one can transfer the study of f(z) at infinity to the study of f(1/z) at the origin.

Note that 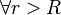\forall r>R, we have

{\mathrm {Res}}(f,\infty )={-1 \over 2\pi i}\int _{{C(0,r)}}f(z)\,dz

See also

References

This article incorporates information from this version of the equivalent article on the French Wikipedia.
  1. ↑ Michèle AUDIN, Analyse Complexe, cursus notes of the university of Strasbourg available on the web, pp. 70–72
  • Murray R. Spiegel, Variables complexes, Schaum, ISBN 2-7042-0020-3
  • Henri Cartan, Théorie analytique des fonctions d'une ou plusieurs varaiables complexes, Hermann, 1961
This article is issued from Wikipedia. The text is available under the Creative Commons Attribution/Share Alike; additional terms may apply for the media files.