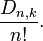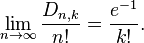Rencontres numbers
In combinatorial mathematics, the rencontres numbers are a triangular array of integers that enumerate permutations of the set { 1, ..., n } with specified numbers of fixed points: in other words, partial derangements. (Rencontre is French for encounter. By some accounts, the problem is named after a solitaire game.) For n ≥ 0 and 0 ≤ k ≤ n, the rencontres number Dn, k is the number of permutations of { 1, ..., n } that have exactly k fixed points.
For example, if seven presents are given to seven different people, but only two are destined to get the right present, there are D7, 2 = 924 ways this could happen. Another often cited example is that of a dance school with 7 couples, where after tea-break the participants are told to randomly find a partner to continue, and there are D7, 2 = 924 possibilities once more, now, that 2 previous couples meet again just by chance.
Numerical values
Here is the beginning of this array (sequence A008290 in OEIS):
 | 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 |
|---|---|---|---|---|---|---|---|---|
| 0 | 1 | |||||||
| 1 | 0 | 1 | ||||||
| 2 | 1 | 0 | 1 | |||||
| 3 | 2 | 3 | 0 | 1 | ||||
| 4 | 9 | 8 | 6 | 0 | 1 | |||
| 5 | 44 | 45 | 20 | 10 | 0 | 1 | ||
| 6 | 265 | 264 | 135 | 40 | 15 | 0 | 1 | |
| 7 | 1854 | 1855 | 924 | 315 | 70 | 21 | 0 | 1 |
Formulas
The numbers in the k = 0 column enumerate derangements. Thus
for non-negative n. It turns out that
where the ratio is rounded up for even n and rounded down for odd n. For n ≥ 1, this gives the nearest integer. More generally, we have
The proof is easy after one knows how to enumerate derangements: choose the k fixed points out of n; then choose the derangement of the other n − k points.
The numbers D<var>n</var>,0/(<var>n</var>!) are generated by the power series e−<var>z</var>/(1 − <var>z</var>); accordingly, an explicit formula for Dn, m can be derived as follows:
This immediately implies that
for n large, m fixed.
Probability distribution
The sum of the entries in each row is the whole number of permutations of { 1, ..., n }, and is therefore n!. If one divides all the entries in the nth row by n!, one gets the probability distribution of the number of fixed points of a uniformly distributed random permutation of { 1, ..., n }. The probability that the number of fixed points is k is
For n ≥ 1, the expected number of fixed points is 1 (a fact that follows from linearity of expectation).
More generally, for i ≤ n, the ith moment of this probability distribution is the ith moment of the Poisson distribution with expected value 1.[1] For i > n, the ith moment is smaller than that of that Poisson distribution. Specifically, for i ≤ n, the ith moment is the ith Bell number, i.e. the number of partitions of a set of size i.
Limiting probability distribution
As the size of the permuted set grows, we get
This is just the probability that a Poisson-distributed random variable with expected value 1 is equal to k. In other words, as n grows, the probability distribution of the number of fixed points of a random permutation of a set of size n approaches the Poisson distribution with expected value 1.
References
- ↑ Jim Pitman, "Some Probabilistic Aspects of Set Partitions", American Mathematical Monthly, volume 104, number 3, March 1997, pages 201–209.
- Riordan, John, An Introduction to Combinatorial Analysis, New York, Wiley, 1958, pages 57, 58, and 65.
- Weisstein, Eric W., "Partial Derangements", MathWorld.

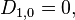

![D_{{n,0}}=\left[{n! \over e}\right]](/2014-wikipedia_en_all_02_2014/I/media/d/6/a/3/d6a38c5b9f46d83ef8310b4288aebe3d.png)

![D_{{n,m}}={\frac {n!}{m!}}[z^{{n-m}}]{\frac {e^{{-z}}}{1-z}}={\frac {n!}{m!}}\sum _{{k=0}}^{{n-m}}{\frac {(-1)^{k}}{k!}}.](/2014-wikipedia_en_all_02_2014/I/media/b/4/b/2/b4b261b04972b22b1dbfc4d9988c130e.png)