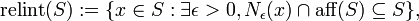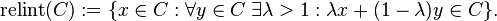Relative interior

From Wikipedia, the free encyclopedia

In mathematics, the relative interior of a set is a refinement of the concept of the interior, which is often more useful when dealing with low-dimensional sets placed in higher-dimensional spaces. Intuitively, the relative interior of a set contains all points which are not on the "edge" of the set, relative to the smallest subspace in which this set lies.

Formally, the relative interior of a set S (denoted 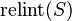\operatorname {relint}(S)) is defined as its interior within the affine hull of S.[1] In other words,

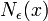\operatorname {relint}(S):=\{x\in S:\exists \epsilon >0,N_{\epsilon }(x)\cap \operatorname {aff}(S)\subseteq S\},

where \operatorname {aff}(S) is the affine hull of S, and N_{\epsilon }(x) is a ball of radius \epsilon centered on x. Any metric can be used for the construction of the ball; all metrics define the same set as the relative interior.

For any nonempty convex sets C\subseteq {\mathbb {R}}^{n} the relative interior can be defined as

\operatorname {relint}(C):=\{x\in C:\forall {y\in C}\;\exists {\lambda >1}:\lambda x+(1-\lambda )y\in C\}.[2][3]

See also

References

  1. ↑ Zălinescu, C. (2002). Convex analysis in general vector spaces. River Edge, NJ: World Scientific Publishing  Co., Inc. pp. 2–3. ISBN 981-238-067-1. MR 1921556. 
  2. ↑ Rockafellar, R. Tyrrell (1997) [1970]. Convex Analysis. Princeton, NJ: Princeton University Press. p. 47. ISBN 978-0-691-01586-6. 
  3. ↑ Dimitri Bertsekas (1999). Nonlinear Programming (2 ed.). Belmont, Massachusetts: Athena Scientific. p. 697. ISBN 978-1-886529-14-4. 
  • Boyd, Stephen; Lieven Vandenberghe (2004). Convex Optimization. Cambridge: Cambridge University Press. p. 23. ISBN 0-521-83378-7. 


This article is issued from Wikipedia. The text is available under the Creative Commons Attribution/Share Alike; additional terms may apply for the media files.