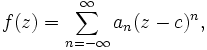Regular part

From Wikipedia, the free encyclopedia

In mathematics, the regular part of a Laurent series consists of the series of terms with positive powers. That is, if

$f(z)=\sum _{{n=-\infty }}^{{\infty }}a_{n}(z-c)^{n},$

then the regular part of this Laurent series is

$\sum _{{n=0}}^{{\infty }}a_{n}(z-c)^{n}.$

In contrast, the series of terms with negative powers is the principal part.

This article is issued from Wikipedia. The text is available under the Creative Commons Attribution/Share Alike; additional terms may apply for the media files.