Regular modal logic

From Wikipedia, the free encyclopedia

In modal logic, a regular modal logic L is a modal logic closed under the duality of the modal operators:

$\Diamond A\equiv \lnot \Box \lnot A$

and the rule

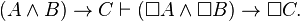
$(A\land B)\to C\vdash (\Box A\land \Box B)\to \Box C.$

Every regular modal logic is classical, and every normal modal logic is regular and hence classical.

References

Chellas, Brian. Modal Logic: An Introduction. Cambridge University Press, 1980.

This article is issued from Wikipedia. The text is available under the Creative Commons Attribution/Share Alike; additional terms may apply for the media files.