Regular homotopy

From Wikipedia, the free encyclopedia

In the mathematical field of topology, a regular homotopy refers to a special kind of homotopy between immersions of one manifold in another. The homotopy must be a 1-parameter family of immersions.

Similar to homotopy classes, one defines two immersions to be in the same regular homotopy class if there exists a regular homotopy between them. Regular homotopy for immersions is similar to isotopy of embeddings: they are both restricted types of homotopies. Stated another way, two continuous functions 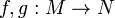$f,g:M\to N$ are homotopic if they represent points in the same path-components of the mapping space $C(M,N)$ , given the compact-open topology. The space of immersions is the subspace of $C(M,N)$ consisting of immersions, denote it by 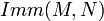$Imm(M,N)$ . 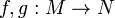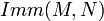Two immersions $f,g:M\to N$ are regularly homotopic if they represent points in the same path-component of $Imm(M,N)$ .

Examples

This curve has total curvature 6π, and turning number 3.

The Whitney–Graustein theorem classifies the regular homotopy classes of a circle into the plane; two immersions are regularly homotopic if and only if they have the same turning number – equivalently, total curvature; equivalently, if and only if their Gauss maps have the same degree/winding number.

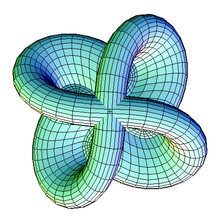
Smale's classification of immersions of spheres shows that sphere eversions exist, which can be realized via this Morin surface.

Stephen Smale classified the regular homotopy classes of a k-sphere immersed in ${\mathbb R}^{n}$ – they are classified by homotopy groups of Stiefel manifolds, which is a generalization of the Gauss map, with here k partial derivatives not vanishing. A corollary of his work is that there is only one regular homotopy class of a 2-sphere immersed in 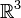${\mathbb R}^{3}$ . In particular, this means that sphere eversions exist, i.e. one can turn the 2-sphere "inside-out".

Both of these examples consist of reducing regular homotopy to homotopy; this has subsequently been substantially generalized in the homotopy principle (or h-principle) approach.

References

Hassler Whitney, On regular closed curves in the plane. Compositio Mathematica, 4 (1937), p. 276–284
Stephen Smale, A classification of immersions of the two-sphere. Trans. Amer. Math. Soc. 90 1958 281–290.
Stephen Smale, The classification of immersions of spheres in Euclidean spaces. Ann. of Math. (2) 69 1959 327–344.

This article is issued from Wikipedia. The text is available under the Creative Commons Attribution/Share Alike; additional terms may apply for the media files.