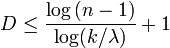Regular graph

From Wikipedia, the free encyclopedia

Graph families defined by their automorphisms
distance-transitive	$\rightarrow$	distance-regular	$\leftarrow$	strongly regular
$\downarrow$
symmetric (arc-transitive)	$\leftarrow$	t-transitive, t ≥ 2
$\downarrow$ _{(if connected)}
vertex- and edge-transitive	$\rightarrow$	edge-transitive and regular	$\rightarrow$	edge-transitive
$\downarrow$		$\downarrow$		$\downarrow$
vertex-transitive	$\rightarrow$	regular	$\rightarrow$	_{(if bipartite)} biregular
$\uparrow$
Cayley graph		skew-symmetric		asymmetric

In graph theory, a regular graph is a graph where each vertex has the same number of neighbors; i.e. every vertex has the same degree or valency. A regular directed graph must also satisfy the stronger condition that the indegree and outdegree of each vertex are equal to each other.^[1] A regular graph with vertices of degree $<var >k</var >$ is called a $<var >k</var >$ ‑regular graph or regular graph of degree $<var >k</var >$ .

Regular graphs of degree at most 2 are easy to classify: A 0-regular graph consists of disconnected vertices, a 1-regular graph consists of disconnected edges, and a 2-regular graph consists of disconnected cycles and infinite chains.

A 3-regular graph is known as a cubic graph.

A strongly regular graph is a regular graph where every adjacent pair of vertices has the same number l of neighbors in common, and every non-adjacent pair of vertices has the same number n of neighbors in common. The smallest graphs that are regular but not strongly regular are the cycle graph and the circulant graph on 6 vertices.

The complete graph 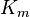$K_{m}$ is strongly regular for any $m$ .

A theorem by Nash-Williams says that every $<var >k</var >$ ‑regular graph on $2<var >k</var > + 1$ vertices has a Hamiltonian cycle.

0-regular graph
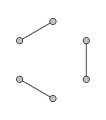
1-regular graph
2-regular graph
3-regular graph

Existence

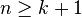It is well known that the necessary and sufficient conditions for a $k$ regular graph of order $n$ to exist are that $n\geq k+1$ and that $nk$ is even. In such case it is easy to construct regular graphs by considering appropriate parameters for circulant graphs.

Algebraic properties

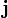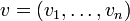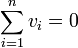Let A be the adjacency matrix of a graph. Then the graph is regular if and only if ${\textbf {j}}=(1,\dots ,1)$ is an eigenvector of A.^[2] Its eigenvalue will be the constant degree of the graph. Eigenvectors corresponding to other eigenvalues are orthogonal to ${\textbf {j}}$ , so for such eigenvectors $v=(v_{1},\dots ,v_{n})$ , we have $\sum _{{i=1}}^{n}v_{i}=0$ .

A regular graph of degree k is connected if and only if the eigenvalue k has multiplicity one.^[2]

There is also a criterion for regular and connected graphs : a graph is connected and regular if and only if the matrix of ones J, with 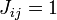$J_{{ij}}=1$ , is in the adjacency algebra of the graph (meaning it is a linear combination of powers of A).^[3]

Let G be a k-regular graph with diameter D and eigenvalues of adjacency matrix $k=\lambda _{0}>\lambda _{1}\geq \dots \geq \lambda _{{n-1}}$ . If G is not bipartite

$D\leq {\frac {\log {(n-1)}}{\log(k/\lambda )}}+1$ ^[4]

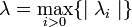where $\lambda =\max _{{i>0}}\{\mid \lambda _{i}\mid \}$ .^[4]

Generation

Regular graphs may be generated by the GenReg program.^[5]

References

↑ Chen, Wai-Kai (1997). Graph Theory and its Engineering Applications. World Scientific. p. 29. ISBN 978-981-02-1859-1.
↑ 2.0 2.1 Cvetković, D. M.; Doob, M.; and Sachs, H. Spectra of Graphs: Theory and Applications, 3rd rev. enl. ed. New York: Wiley, 1998.
↑ Curtin, Brian (2005), "Algebraic characterizations of graph regularity conditions", Designs, Codes and Cryptography 34 (2-3): 241–248, doi:10.1007/s10623-004-4857-4, MR 2128333 .
↑ 4.0 4.1 http://personal.plattsburgh.edu/quenelgt/pubpdf/diamest.pdf
↑ Meringer, Markus (1999). "Fast generation of regular graphs and construction of cages". Journal of Graph Theory 30 (2): 137–146. doi:10.1002/(SICI)1097-0118(199902)30:2<>1.0.CO;2-G.

External links

Wikimedia Commons has media related to Regular graphs.

Weisstein, Eric W., "Regular Graph", MathWorld.
Weisstein, Eric W., "Strongly Regular Graph", MathWorld.
GenReg software and data by Markus Meringer.
Nash-Williams, Crispin (1969). "Valency Sequences which force graphs to have Hamiltonian Circuits". University of Waterloo Research Report. Waterloo, Ontario: University of Waterloo

This article is issued from Wikipedia. The text is available under the Creative Commons Attribution/Share Alike; additional terms may apply for the media files.