Region (mathematical analysis)

From Wikipedia, the free encyclopedia

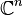In mathematical analysis, the word region usually refers to a subset of \mathbb{R} ^{n} or \mathbb{C} ^{n} that is open (in the standard Euclidean topology), connected and non-empty. A closed region is sometimes defined to be the closure of a region.

Regions and closed regions are often used as domains of functions or differential equations.

According to Kreyszig,[1]

A region is a set consisting of a domain plus, perhaps, some or all of its boundary points. (The reader is warned that some authors use the term "region" for what we call a domain [following standard terminology], and others make no distinction between the two terms.)

According to Yue Kuen Kwok,

An open connected set is called an open region or domain. ...to an open region we may add none, some, or all its limit points, and simply call the new set a region.[2]

See also

Notes and references

  1. ↑ Erwin Kreyszig (1993) Advanced Engineering Mathematics, 7th edition, p. 720, John Wiley & Sons, ISBN 0-471-55380-8
  2. ↑ Yue Kuen Kwok (2002) Applied Complex Variables for Scientists and Engineers, § 1.4 Some topological definitions, p 23, Cambridge University Press, ISBN 0-521-00462-4
  • Ruel V. Churchill (1960) Complex variables and applications, 2nd edition, §1.9 Regions in the complex plane, pp. 16 to 18, McGraw-Hill
  • Constantin Carathéodory (1954) Theory of Functions of a Complex Variable, v. I, p. 97, Chelsea Publishing.
  • Howard Eves (1966) Functions of a Complex Variable, p. 105, Prindle, Weber & Schmidt.
This article is issued from Wikipedia. The text is available under the Creative Commons Attribution/Share Alike; additional terms may apply for the media files.