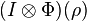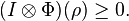Reduction criterion

From Wikipedia, the free encyclopedia

In quantum information theory, the reduction criterion is a necessary condition a mixed state must satisfy in order for it to be separable. In other words, the reduction criterion is a separability criterion. It was fist proved in ^[1] and independently formulated in.^[2] Violation of the reduction criterion is closely related to the distillability of the state in question.^[1]

Details

Let H₁ and H₂ be Hilbert spaces of finite dimensions n and m respectively. L(H_i) will denote the space of linear operators acting on H_i. Consider a bipartite quantum system whose state space is the tensor product

$H=H_{1}\otimes H_{2}.$

An (un-normalized) mixed state ρ is a positive linear operator (density matrix) acting on H.

A linear map Φ: L(H₂) → L(H₁) is said to be positive if it preserves the cone of positive elements, i.e. A is positive implied Φ(A) is also.

From the one-to-one correspondence between positive maps and entanglement witnesses, we have that a state ρ is entangled if and only if there exists a positive map Φ such that

$(I\otimes \Phi )(\rho )$

is not positive. Therefore, if ρ is separable, then for all positive map Φ,

$(I\otimes \Phi )(\rho )\geq 0.$

Thus every positive, but not completely positive, map Φ gives rise to a necessary condition for separability in this way. The reduction criterion is a particular example of this.

Suppose H₁ = H₂. Define the positive map Φ: L(H₂) → L(H₁) by

$\Phi (A)=\operatorname {Tr}A-A.$

It is known that Φ is positive but not completely positive. So a mixed state ρ being separable implies

$(I\otimes \Phi )(\rho )\geq 0.$

Direct calculation shows that the above expression is the same as

$I\otimes \rho _{1}-\rho \geq 0$

where ρ₁ is the partial trace of ρ with respect to the second system. The dual relation

$\rho _{2}\otimes I-\rho \geq 0$

is obtained in the analogous fashion. The reduction criterion consists of the above two inequalities. The reduction criterion is

References

↑ 1.0 1.1 M. Horodecki and P. Horodecki (1999). "Reduction criterion of separability and limits for a class of distillation protocols". Phys. Rev. A. 59: 4206. arXiv:quant-ph/9708015. doi:10.1103/PhysRevA.59.4206.
↑ N. Cerf et al. (1999). "Reduction criterion for separability". Phys. Rev. A. 60: 898. arXiv:quant-ph/9710001. doi:10.1103/PhysRevA.60.898.

This article is issued from Wikipedia. The text is available under the Creative Commons Attribution/Share Alike; additional terms may apply for the media files.