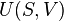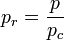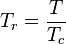Reduced properties

Thermodynamics
The classical Carnot heat engine Book:Thermodynamics
Branches Classical Statistical Chemical Equilibrium / Non-equilibrium
Laws Zeroth First Second Third
Systems State Equation of state Ideal gas Real gas Phase / State of matter Equilibrium Control volume Instruments Processes Isobaric Isochoric Isothermal Adiabatic Isentropic Isenthalpic Quasistatic Polytropic Free expansion Reversibility Irreversibility Endoreversibility Cycles Heat engines Heat pumps Thermal efficiency
System properties Property diagrams Intensive and extensive properties Functions of state (Conjugate variables in italics) Temperature / Entropy Introduction to entropy Pressure / Volume Chemical potential / Particle number Vapor quality Reduced properties Process functions Work Heat
Material properties Specific heat capacity  Compressibility  Thermal expansion  Property database
Equations Carnot's theorem Clausius theorem Fundamental relation Ideal gas law Maxwell relations Onsager reciprocal relations Bridgman's thermodynamic equations Table of thermodynamic equations
Potentials Free energy Free entropy Internal energy Enthalpy Helmholtz free energy Gibbs free energy
History / Culture Philosophy Entropy and time Entropy and life Brownian ratchet Maxwell's demon Heat death paradox Loschmidt's paradox Synergetics History General Heat Entropy Gas laws "Perpetual motion" machines Theories Caloric theory Vis viva Theory of heat Mechanical equivalent of heat Motive power Key publications "An Experimental Enquiry Concerning ... Heat" "On the Equilibrium of Heterogeneous Substances" "Reflections on the Motive Power of Fire" Timelines Thermodynamics Heat engines Art Maxwell's thermodynamic surface Education Entropy as energy dispersal
Scientists Bernoulli Carnot Clapeyron Clausius Carathéodory Pierre Duhem Gibbs von Helmholtz Joule Maxwell von Mayer Onsager Rankine Smeaton Stahl Thompson Thomson (Baron Kelvin) Waterson saha
v t e

In thermodynamics, the reduced properties of a fluid are a set of state variables normalized by the fluid's state properties at its critical point. These dimensionless thermodynamic coordinates, taken together with a substance's compressibility factor, provide the basis for the simplest form of the theorem of corresponding states.^[1]

Reduced properties are also used to define the Peng-Robinson equation of state, a model designed to provide reasonable accuracy near the critical point.^[2] They are also used to critical exponents, which describe the behaviour of physical quantities near continuous phase transitions.^[3]

Reduced pressure

The reduced pressure is defined as its actual pressure divided by its critical pressure :^[1]

Reduced temperature

The reduced temperature of a fluid is its actual temperature, divided by its critical temperature:^[1]

where the actual temperature and critical temperature are expressed in absolute temperature scales (either Kelvin or Rankine). Both the reduced temperature and the reduced pressure are often used in thermodynamical formulas like the Peng-Robinson equation of state.

Reduced specific volume

The reduced specific volume (or "pseudo-reduced specific volume") of a fluid is computed from the ideal gas law at the substance's critical pressure and temperature:^[1]

This property is useful when the specific volume and either temperature or pressure are known, in which case the missing third property can be computed directly.

See also

• Departure function

References