Rectified cubic honeycomb
| Rectified cubic honeycomb | |
|---|---|
  | |
| Type | Uniform honeycomb |
| Cells | Octahedron  Cuboctahedron  |
| Schläfli symbol | r{4,3,4} t1{4,3,4} |
| Coxeter-Dynkin diagrams |     |
| Vertex figure |  Cuboid |
| Space group Fibrifold notation | Pm3m (221) 4−:2 |
| Coxeter group |  , [4,3,4] |
| Dual | oblate octahedrille (Square bipyramidal honeycomb) |
| Properties | vertex-transitive, edge-transitive |
The rectified cubic honeycomb is a uniform space-filling tessellation (or honeycomb) in Euclidean 3-space. It is composed of octahedra and cuboctahedra in a ratio of 1:1.
John Horton Conway calls this honeycomb a cuboctahedrille, and its dual oblate octahedrille.
Symmetry
There are four uniform colorings for the cells of this honeycomb with reflective symmetry, listed by their Coxeter group, and Wythoff construction name, and the Coxeter-Dynkin diagram below.
| Symmetry | [4,3,4], =<<[3[4]]>> |
[4,31,1],  =<[3[4]]>1 |
[4,31,1], =<[3[4]]>2 |
[3[4]],  |
|---|---|---|---|---|
| Space group | Pm3m (221) | Fm3m (225) | Fm3m (225) | F43m (216) |
| Coloring |  |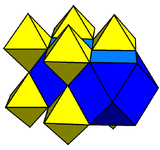
 |
 |
 |
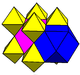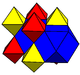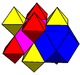| Coxeter diagram |
|
  |
  | |
|
|
| ||
| Vertex figure | |
 |
 |
 |
| Vertex figure symmetry |
[4,2] order 16 |
[2,2] order 8 |
[4] order 8 |
[2] order 4 |
Related honeycombs
The [4,31,1], , Coxeter group generates 9 permutations of uniform tessellations, 4 with distinct geometry including the alternated cubic honeycomb.
| Space group |
Fibrifold | Extended symmetry |
Extended diagram |
Order | Honeycombs |
|---|---|---|---|---|---|
| Fm3m (225) |
2−:2 | [4,31,1] = [4,3,4,1+] |
   =  |
×1 | 1, 2, 3, 4 |
| Fm3m (225) |
2−:2 | <[1+,4,31,1]> = <[3[4]]> |
 = |
×2 | (1), (3) |
| Pm3m (221) |
4−:2 | <[4,31,1]> |  |
×2 |
This honeycomb is one of five distinct uniform honeycombs[1] constructed by the Coxeter group. The symmetry can be multiplied by the symmetry of rings in the Coxeter–Dynkin diagrams:
| Space group |
Fibrifold | Square symmetry |
Extended symmetry |
Extended diagram |
Extended order |
Honeycomb diagrams |
|---|---|---|---|---|---|---|
| F43m (216) |
1o:2 | a1 | [3[4]] | |
×1 | (None) |
| Fd3m (227) |
2+:2 | p2 | [[3[4]]] |    = |
×2 | 3 |
| Fm3m (225) |
2−:2 | d2 | <[3[4]]> = [4,3,31,1] |
 = |
×2 |  1, 2 |
| Pm3m (221) |
4−:2 | d4 | [2[3[4]]] = [4,3,4] |
 = |
×4 | 4 |
| Im3m (229) |
8o:2 | r8 | [4[3[4]]] = [[4,3,4]] |
 =  |
×8 | 5,  (*) |
See also
References
 |
Wikimedia Commons has media related to Rectified cubic honeycomb. |
- John H. Conway, Heidi Burgiel, Chaim Goodman-Strauss, (2008) The Symmetries of Things, ISBN 978-1-56881-220-5 (Chapter 21, Naming the Archimedean and Catalan polyhedra and tilings, Architectonic and Catoptric tessellations, p 292-298, includes all the nonprismatic forms)
- George Olshevsky, Uniform Panoploid Tetracombs, Manuscript (2006) (Complete list of 11 convex uniform tilings, 28 convex uniform honeycombs, and 143 convex uniform tetracombs)
- Branko Grünbaum, Uniform tilings of 3-space. Geombinatorics 4(1994), 49 - 56.
- Kaleidoscopes: Selected Writings of H.S.M. Coxeter, edited by F. Arthur Sherk, Peter McMullen, Anthony C. Thompson, Asia Ivic Weiss, Wiley-Interscience Publication, 1995, ISBN 978-0-471-01003-6
- (Paper 22) H.S.M. Coxeter, Regular and Semi Regular Polytopes I, [Math. Zeit. 46 (1940) 380-407, MR 2,10] (1.9 Uniform space-fillings)
- A. Andreini, Sulle reti di poliedri regolari e semiregolari e sulle corrispondenti reti correlative (On the regular and semiregular nets of polyhedra and on the corresponding correlative nets), Mem. Società Italiana della Scienze, Ser.3, 14 (1905) 75–129.
- Richard Klitzing, 3D Euclidean Honeycombs, o4x3o4o - rich - O15
- Uniform Honeycombs in 3-Space: 02-Rich