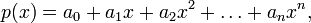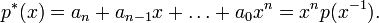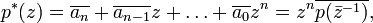Reciprocal polynomial

From Wikipedia, the free encyclopedia

In the mathematical area of algebra, given a polynomial p with coefficients from an arbitrary field such as:

$p(x)=a_{0}+a_{1}x+a_{2}x^{2}+\ldots +a_{n}x^{n},\,\!$

we define the reciprocal polynomial, p*by:^[1]

$p^{*}(x)=a_{n}+a_{{n-1}}x+\ldots +a_{0}x^{n}=x^{n}p(x^{{-1}}).$

Essentially, the coefficients are written in reverse order.

In the special case that the polynomial p has complex coefficients, that is,

$p(z)=a_{0}+a_{1}z+a_{2}z^{2}+\ldots +a_{n}z^{n},\,\!$

the conjugate reciprocal polynomial, p* given by,

$p^{*}(z)=\overline {a_{n}}+\overline {a_{{n-1}}}z+\ldots +\overline {a_{0}}z^{n}=z^{n}\overline {p({\bar {z}}^{{-1}})},$

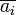where $\overline {a_{i}}$ denotes the complex conjugate of 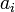$a_{i}\,\!$ , is called the reciprocal polynomial when no confusion can arise.

A polynomial is called self-reciprocal if 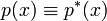$p(x)\equiv p^{{*}}(x)$ .

The coefficients of a self-reciprocal polynomial satisfy a_i = a_n−i, and in this case p is also called a palindromic polynomial. In the conjugate reciprocal case, the coefficients must be real to satisfy the condition.

Properties

Reciprocal polynomials have several connections with their original polynomials, including:

α is a root of polynomial p if and only if α⁻¹ is a root of p*.^[2]
If p(x) ≠ x then p is irreducible if and only if p* is irreducible.^[3]
p is primitive if and only if p* is primitive.^[4]

Other properties of reciprocal polynomials may be obtained, for instance:

If a polynomial is self-reciprocal and irreducible then it must have even degree.^[5]

Properties of conjugate reciprocal polynomials

If p(z) is the minimal polynomial of z₀ with |z₀| = 1, 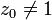$z_{0}\neq 1$ , and p(z) has real coefficients, then p(z) is self-reciprocal. This follows because

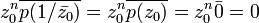$z_{0}^{n}\overline {p(1/{\bar {z_{0}}})}=z_{0}^{n}\overline {p(z_{0})}=z_{0}^{n}{\bar {0}}=0$ .

So z₀ is a root of the polynomial 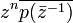$z^{n}\overline {p({\bar {z}}^{{-1}})}$ which has degree n. But, the minimal polynomial is unique, hence

$cp(z)=z^{n}\overline {p({\bar {z}}^{{-1}})}$

for some constant c, i.e. 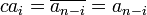$ca_{i}=\overline {a_{{n-i}}}=a_{{n-i}}$ . Sum from i = 0 to n and note that 1 is not a root of p. We conclude that c = 1.

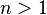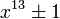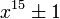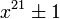A consequence is that the cyclotomic polynomials $\Phi _{n}$ are self-reciprocal for $n>1$ ; this is used in the special number field sieve to allow numbers of the form $x^{{11}}\pm 1$ , $x^{{13}}\pm 1$ , $x^{{15}}\pm 1$ and $x^{{21}}\pm 1$ to be factored taking advantage of the algebraic factors by using polynomials of degree 5, 6, 4 and 6 respectively - note that $\phi$ (Euler's totient function) of the exponents are 10, 12, 8 and 12.

Application in coding theory

The reciprocal polynomial finds a use in the theory of cyclic error correcting codes. Suppose xⁿ - 1 can be factored into the product of two polynomials, say xⁿ - 1 = g(x)p(x). When g(x) generates a cyclic code C, then the reciprocal polynomial p*(x) generates C^⊥, the orthogonal complement of C.^[6] Also, C is self-orthogonal (that is, C ⊆ C^⊥), if and only if p*(x) divides g(x).^[7]

Notes

↑ Roman 1995, pg.37
↑ Pless 1990, pg. 57
↑ Roman 1995, pg. 37
↑ Pless 1990, pg. 57
↑ Roman 1995, pg. 37
↑ Pless 1990, pg. 75, Theorem 48
↑ Pless 1990, pg. 77, Theorem 51

References

Pless, Vera (1990), Introduction to the Theory of Error Correcting Codes (2nd ed.), New York: Wiley-Interscience, ISBN 0-471-61884-5

Roman, Steven (1995), Field Theory, New York: Springer-Verlag, ISBN 0-387-94408-7

External links

Reciprocal Polynomial (on MathWorld)

This article is issued from Wikipedia. The text is available under the Creative Commons Attribution/Share Alike; additional terms may apply for the media files.