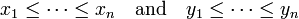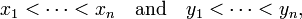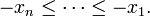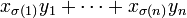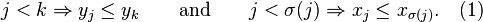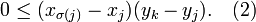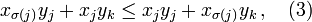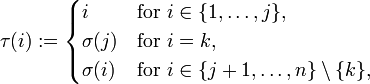Rearrangement inequality

From Wikipedia, the free encyclopedia

In mathematics, the rearrangement inequality[1] states that

x_{n}y_{1}+\cdots +x_{1}y_{n}\leq x_{{\sigma (1)}}y_{1}+\cdots +x_{{\sigma (n)}}y_{n}\leq x_{1}y_{1}+\cdots +x_{n}y_{n}

for every choice of real numbers

x_{1}\leq \cdots \leq x_{n}\quad {\text{and}}\quad y_{1}\leq \cdots \leq y_{n}

and every permutation

x_{{\sigma (1)}},\dots ,x_{{\sigma (n)}}\,

of x1, . . ., xn. If the numbers are different, meaning that

x_{1}<\cdots <x_{n}\quad {\text{and}}\quad y_{1}<\cdots <y_{n},

then the lower bound is attained only for the permutation which reverses the order, i.e. σ(i) = n − i + 1 for all i = 1, ..., n, and the upper bound is attained only for the identity, i.e. σ(i) = i for all i = 1, ..., n.

Note that the rearrangement inequality makes no assumptions on the signs of the real numbers.

Applications

Many famous inequalities can be proved by the rearrangement inequality, such as the arithmetic mean – geometric mean inequality, the Cauchy–Schwarz inequality, and Chebyshev's sum inequality.

Proof

The lower bound follows by applying the upper bound to

-x_{n}\leq \cdots \leq -x_{1}.

Therefore, it suffices to prove the upper bound. Since there are only finitely many permutations, there exists at least one for which

x_{{\sigma (1)}}y_{1}+\cdots +x_{{\sigma (n)}}y_{n}

is maximal. In case there are several permutations with this property, let σ denote one with the highest number of fixed points.

We will now prove by contradiction, that σ has to be the identity (then we are done). Assume that σ is not the identity. Then there exists a j in {1, ..., n − 1} such that σ(j) ≠ j and σ(i) = i for all i in {1, ..., j − 1}. Hence σ(j) > j and there exists k in {j + 1, ..., n} with σ(k) = j. Now

j<k\Rightarrow y_{j}\leq y_{k}\qquad {\text{and}}\qquad j<\sigma (j)\Rightarrow x_{j}\leq x_{{\sigma (j)}}.\quad (1)

Therefore,

0\leq (x_{{\sigma (j)}}-x_{j})(y_{k}-y_{j}).\quad (2)

Expanding this product and rearranging gives

x_{{\sigma (j)}}y_{j}+x_{j}y_{k}\leq x_{j}y_{j}+x_{{\sigma (j)}}y_{k}\,,\quad (3)

hence the permutation

\tau (i):={\begin{cases}i&{\text{for }}i\in \{1,\ldots ,j\},\\\sigma (j)&{\text{for }}i=k,\\\sigma (i)&{\text{for }}i\in \{j+1,\ldots ,n\}\setminus \{k\},\end{cases}}

which arises from σ by exchanging the values σ(j) and σ(k), has at least one additional fixed point compared to σ, namely at j, and also attains the maximum. This contradicts the choice of σ.

If

x_{1}<\cdots <x_{n}\quad {\text{and}}\quad y_{1}<\cdots <y_{n},

then we have strict inequalities at (1), (2), and (3), hence the maximum can only be attained by the identity, any other permutation σ cannot be optimal.

See also

References

  1. ↑ Hardy, G.H.; Littlewood, J.E.; Pólya, G. (1952), Inequalities, Cambridge Mathematical Library (2. ed.), Cambridge: Cambridge University Press, ISBN 0-521-05206-8, MR 0046395, Zbl 0047.05302 , Section 10.2, Theorem 368
This article is issued from Wikipedia. The text is available under the Creative Commons Attribution/Share Alike; additional terms may apply for the media files.