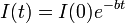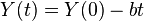Reactive inhibition

From Wikipedia, the free encyclopedia

Reactive inhibition is a phrase coined by Clark L. Hull (1951) in his postulate X.A.:

Whenever a reaction R is evoked from an organism there is left an increment of primary negative drive I_R which inhibits to a degree according to its magnitude the reaction potential_SE_R to that response (Hull, 1951, p. 74).

According to Hull's postulate X.B. inhibition I dissipates exponentially with time t:.:

With the passage of time since its formation I_R spontaneously dissipates approximately as a simple decay function of the time t elapsed, i.e.,
$I'_{R}=I_{R}x10^{{-at}}$ (Hull, 1951, p. 74).

Hull's decay formula is somewhat awkward and might give rise to confusion. For example, I'_R does not refer to the derivative of I_R. A more convenient way of writing the formula would be as follows:

$I(t)=I(0)e^{{-bt}}$

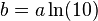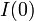with $b=a\ln(10)$ . $I(0)$ is the inhibition at the beginning the time interval [0,t]. Note, that if one takes the natural logarithm of both sides one obtains:

$Y(t)=Y(0)-bt$

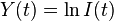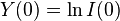where $Y(t)=\ln I(t)$ and $Y(0)=\ln I(0)$ . The last formula is used in Inhibition Theory.

References

Hull, C.L.: Essentials of behavior. Westport (Connecticut): Greenwood Press, 1951.

This article is issued from Wikipedia. The text is available under the Creative Commons Attribution/Share Alike; additional terms may apply for the media files.