Rational singularity

From Wikipedia, the free encyclopedia

In mathematics, more particularly in the field of algebraic geometry, a scheme $X$ has rational singularities, if it is normal, of finite type over a field of characteristic zero, and there exists a proper birational map

$f\colon Y\rightarrow X$

from a regular scheme $Y$ such that the higher direct images of $f_{*}$ applied to ${\mathcal {O}}_{Y}$ are trivial. That is,

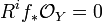$R^{i}f_{*}{\mathcal {O}}_{Y}=0$ for $i>0$ .

If there is one such resolution, then it follows that all resolutions share this property, since any two resolutions of singularities can be dominated by a third.

For surfaces, rational singularities were defined by (Artin 1966).

Formulations

Alternately, one can say that $X$ has rational singularities if and only if the natural map in the derived category

${\mathcal {O}}_{X}\rightarrow Rf_{*}{\mathcal {O}}_{Y}$

is a quasi-isomorphism. Notice that this includes the statement that ${\mathcal {O}}_{X}\simeq f_{*}{\mathcal {O}}_{Y}$ and hence the assumption that $X$ is normal.

There are related notions in positive and mixed characteristic of

pseudo-rational

and

F-rational

Rational singularities are in particular Cohen-Macaulay, normal and Du Bois. They need not be Gorenstein or even Q-Gorenstein.

Log terminal singularities are rational.^{[citation needed]}

Examples

An example of a rational singularity is the singular point of the quadric cone

$x^{2}+y^{2}+z^{2}=0.\,$

(Artin 1966) showed that the rational double points of a algebraic surfaces are the Du Val singularities.

References

Artin, Michael (1966), "On isolated rational singularities of surfaces", American Journal of Mathematics (The Johns Hopkins University Press) 88 (1): 129–136, doi:10.2307/2373050, ISSN 0002-9327, JSTOR 2373050, MR 0199191
Lipman, Joseph (1969), "Rational singularities, with applications to algebraic surfaces and unique factorization", Publications Mathématiques de l'IHÉS (36): 195–279, ISSN 1618-1913, MR 0276239

This article is issued from Wikipedia. The text is available under the Creative Commons Attribution/Share Alike; additional terms may apply for the media files.