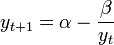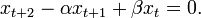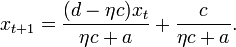Rational difference equation

From Wikipedia, the free encyclopedia

A rational difference equation is a nonlinear difference equation of the form^[1]^[2]

$x_{{n+1}}={\frac {\alpha +\sum _{{i=0}}^{k}\beta _{i}x_{{n-i}}}{A+\sum _{{i=0}}^{k}B_{i}x_{{n-i}}}},$

where the initial conditions 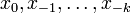$x_{{0}},x_{{-1}},\dots ,x_{{-k}}$ are such that the denominator is never zero for any $n$ .

First-order rational difference equation

A first-order rational difference equation is a nonlinear difference equation of the form

$w_{{t+1}}={\frac {aw_{t}+b}{cw_{t}+d}}.$

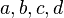When $a,b,c,d$ and the initial condition 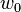$w_{{0}}$ are real numbers, this difference equation is called a Riccati difference equation.^[2]

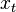Such an equation can be solved by writing $w_{t}$ as a nonlinear transformation of another variable $x_{t}$ which itself evolves linearly. Then standard methods can be used to solve the linear difference equation in $x_{t}$ .

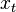Solving a first-order equation

First approach

One approach ^[3] to developing the transformed variable 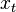$x_{t}$ , when 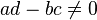$ad-bc\neq 0$ , is to write

$y_{{t+1}}=\alpha -{\frac {\beta }{y_{t}}}$

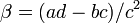where $\alpha =(a+d)/c$ and $\beta =(ad-bc)/c^{{2}}$ and where 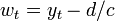$w_{t}=y_{t}-d/c$ . Further writing 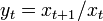$y_{t}=x_{{t+1}}/x_{t}$ can be shown to yield

$x_{{t+2}}-\alpha x_{{t+1}}+\beta x_{t}=0.\,$

Second approach

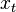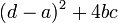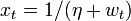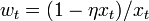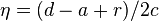This approach ^[4] gives a first-order difference equation for $x_{t}$ instead of a second-order one, for the case in which $(d-a)^{{2}}+4bc$ is non-negative. Write $x_{t}=1/(\eta +w_{t})$ implying $w_{t}=(1-\eta x_{t})/x_{t}$ , where $\eta$ is given by $\eta =(d-a+r)/2c$ and where 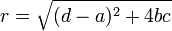$r={\sqrt {(d-a)^{{2}}+4bc}}$ . Then it can be shown that 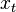$x_{t}$ evolves according to

$x_{{t+1}}={\frac {(d-\eta c)x_{t}}{\eta c+a}}+{\frac {c}{\eta c+a}}.$

Application

It was shown in ^[5] that a dynamic matrix Riccati equation of the form

$H_{{t-1}}=K+A'H_{t}A-A'H_{t}C(C'H_{t}C)^{{-1}}C'H_{t}A,\,$

which can arise in some discrete-time optimal control problems, can be solved using the second approach above if the matrix C has only one more row than column.

References

↑ Dynamics of third-order rational difference equations with open problems and Conjectures
↑ 2.0 2.1 Dynamics of Second-order rational difference equations with open problems and Conjectures
↑ Brand, Louis, "A sequence defined by a difference equation," American Mathematical Monthly 62, September 1955, 489–492.
↑ Mitchell, Douglas W., "An analytic Riccati solution for two-target discrete-time control," Journal of Economic Dynamics and Control 24, 2000, 615–622.
↑ Balvers, Ronald J., and Mitchell, Douglas W., "Reducing the dimensionality of linear quadratic control problems," Journal of Economic Dynamics and Control 31, 2007, 141–159.