Random laser
A random laser is a laser that uses a highly disordered gain medium. A random laser uses no optical cavity but the remaining principles of operation remain the same as for a conventional laser. Random laser action has been observed in many different media, including semiconductor powder, nanostructured and non-nanostructured thin films, laser dyes, ceramics and many more.
Developments in nanoparticles have demonstrated that large amounts of optical scattering can occur when photons are incident. In this way, light can be diffused around a medium in much the same way as it is on white paint and in clouds.
Incoherent regime
If nano particles are embedded in an optical gain medium, for example, zinc oxide (UV emission - bandgap 3.3 eV), light from a pump source ( e.g. frequency-tripled Nd:YAG laser) will induce spontaneous emission of light at around 350 nm within the gain medium. These spontaneously emitted photons will then stimulate other radiative transitions in the gain medium to take place, unleashing yet more photons. This is, in many ways analogous to the chain reaction that occurs in the fission of neutrons in a nuclear reactor and has been referred to by R.H. Dicke as an "optical bomb".[1]
Anderson localization
Anderson localization is a well-known phenomenon which occurs when electrons become trapped in a disordered metallic structure and this metal goes through a phase transition from conductor to insulator.[2] These electrons are said to be Anderson Localized. The conditions for this localization are that there is a high enough density of scatters in the metal (other electrons, spins, etc.) to cause free electrons to follow a single looped path.
In analogy to this, we can imagine photons diffusing through a medium scattering off nanoparticles of diameter 10 - 100 nm. If the Ioffe-Regel[citation needed] criterion, describing the ratio of photon wave-vector k to mean free-path length (of a photon not colliding with anything) l, is met: 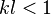 , then there is a probability that photons will become trapped in much the same way as electrons are observed to be trapped under Anderson localization. In this way, while the photon is trapped, the scatters may act as an optical cavity. The gain medium in which the scatterers lie will allow for stimulated emission to occur. As in an ordinary laser, if the gain is greater than the losses incurred, the lasing threshold will be broken and lasing can occur.
, then there is a probability that photons will become trapped in much the same way as electrons are observed to be trapped under Anderson localization. In this way, while the photon is trapped, the scatters may act as an optical cavity. The gain medium in which the scatterers lie will allow for stimulated emission to occur. As in an ordinary laser, if the gain is greater than the losses incurred, the lasing threshold will be broken and lasing can occur.
Photons traveling in this loop will also interfere with each other. The well defined cavity length (1- 10 μm) will ensure that the interference is constructive and will allow certain modes to oscillate. The competition for gain permits one mode to oscillate once the lasing threshold has been reached.
Random Laser Theory
Theory however shows that for multiple scattering in amplifying random media "Anderson" localization of light does not occur at all - even though the calculation of interferences are essential to prove that fact. In contrary so called weak localizations processes can be proven, but it is vividly discussed, whether those mechanisms play the key role in the mode statistics or not.[citation needed]
Recent studies[citation needed] show that these weak localization processes are not the governing phenomena for the onset of Random Lasing. Random Lasing occurs for 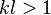 ![citation needed] This is in agreement with experimental findings.[citation needed] Even though travelling of light on exactly 'closed loops' would explain the occurrence of confined lasing spots intuitively, the question is still open if, e.g. the stimulated emission processes are correlated with those processes.[citation needed]
![citation needed] This is in agreement with experimental findings.[citation needed] Even though travelling of light on exactly 'closed loops' would explain the occurrence of confined lasing spots intuitively, the question is still open if, e.g. the stimulated emission processes are correlated with those processes.[citation needed]
The theory of 'preformed cavities' is however not confirmed.
Typical amounts of gain medium required to exceed the lasing threshold depend heavily on the scatterer density.
Applications
This field is relatively young and as such does not have many realized applications. However, random lasers based on ZnO are promising candidates for electrically pumped UV lasers, biosensors and optical information processing. This is due to the low production cost and that the optimum temperature for substrate production has been observed to be around 500°C for powders. This is in contrast to producing an ordinary laser crystal at temperatures exceeding 700°C.