Random element

From Wikipedia, the free encyclopedia

In probability theory, random element is a generalization of the concept of random variable to more complicated spaces than the simple real line. The concept was introduced by Maurice Fréchet (1948) who commented that the “development of probability theory and expansion of area of its applications have led to necessity to pass from schemes where (random) outcomes of experiments can be described by number or a finite set of numbers, to schemes where outcomes of experiments represent, for example, vectors, functions, processes, fields, series, transformations, and also sets or collections of sets.” ^{[citation needed]}

The modern day usage of “random element” frequently assumes the space of values is a topological vector space, often a Banach or Hilbert space with a specified natural sigma algebra of subsets.

Definition

Let (Ω, ℱ, P) be a probability space, and (E, ℰ) a measurable space. A random element with values in E is a function X: Ω→E which is (ℱ, ℰ)-measurable. That is, a function X such that for any B ∈ ℰ the preimage of B lies in ℱ: {ω: X(ω) ∈ B} ∈ ℱ.

Sometimes random elements with values in $E$ are called $E$ -valued random variables.

Note if 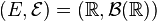$(E,{\mathcal {E}})=({\mathbb {R}},{\mathcal {B}}({\mathbb {R}}))$ , where 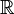${\mathbb {R}}$ are the real numbers, and 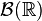${\mathcal {B}}({\mathbb {R}})$ is its Borel σ-algebra, then the definition of random element is the classical definition of random variable.

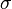The definition of a random element $X$ with values in a Banach space $B$ is typically understood to utilize the smallest $\sigma$ -algebra on B for which every bounded linear functional is measurable. An equivalent definition, in this case, to the above, is that a map 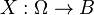$X:\Omega \rightarrow B$ , from a probability space, is a random element if 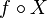$f\circ X$ is a random variable for every bounded linear functional f, or, equivalently, that $X$ is weakly measurable.

List of different types of random elements

Random variable
Discrete random variable
Continuous random variable
Complex random variable
Simple random variable
Random vector
Random matrix
Random function
Random process
Random field
Random measure
Random set
Random closed set
Random compact set
Random “point”
Random figure^[1]
Random shape^[1]
Random finite set
Random finite abstract set
Random set of events

References

↑ 1.0 1.1 Stoyan, D., and Stoyan, H. (1994) Fractals, Random Shapes and Point Fields. Methods of Geometrical Statistics. Chichester, New York: John Wiley & Sons. ISBN 0-471-93757-6

Literature

Fréchet, M. (1948). "Les éléments aléatoires de nature quelconque dans un espace distancié". Annales de l'Institut Henri Poincaré 10 (4): 215–310.
Hoffman-Jorgensen J., Pisier G. (1976) "Ann.Probab.", v.4, 587-589.
Mourier E. (1955) Elements aleatoires dans un espace de Banach (These). Paris.
Prokhorov Yu.V. (1999) Random element. Probability and Mathematical statistics. Encyclopedia. Moscow: "Great Russian Encyclopedia", P.623.

External links

Entry in Springer Encyclopedia of Mathematics

This article is issued from Wikipedia. The text is available under the Creative Commons Attribution/Share Alike; additional terms may apply for the media files.