Radon's theorem

From Wikipedia, the free encyclopedia

In geometry, Radon's theorem on convex sets, named after Johann Radon, states that any set of d + 2 points in Rd can be partitioned into two (disjoint) sets whose convex hulls intersect. A point in the intersection of these hulls is called a Radon point of the set.

For example, in the case d = 2, any set of four points in the Euclidean plane can be partitioned in one of two ways. It may form a triple and a singleton, where the convex hull of the triple (a triangle) contains the singleton; alternatively, it may form two pairs of points that form the endpoints of two intersecting line segments.

Proof and construction

Two sets of four points in the plane (the vertices of a square and an equilateral triangle with its centroid), the multipliers solving the system of three linear equations for these points, and the Radon partitions formed by separating the points with positive multipliers from the points with negative multipliers.

Consider any set 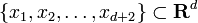\{x_{1},x_{2},\dots ,x_{{d+2}}\}\subset {\mathbf {R}}^{d} of d + 2 points in d-dimensional space. Then there exists a set of multipliers a1, ..., ad + 2, not all of which are zero, solving the system of linear equations

\sum _{{i=1}}^{{d+2}}a_{i}x_{i}=0,\quad \sum _{{i=1}}^{{d+2}}a_{i}=0,

because there are d + 2 unknowns (the multipliers) but only d + 1 equations that they must satisfy (one for each coordinate of the points, together with a final equation requiring the sum of the multipliers to be zero). Fix some particular nonzero solution a1, ..., ad + 2. Let I be the set of points with positive multipliers, and let J be the set of points with multipliers that are negative or zero. Then I and J form the required partition of the points into two subsets with intersecting convex hulls.

The convex hulls of I and J must intersect, because they both contain the point

p=\sum _{{i\in I}}{\frac {a_{i}}{A}}x_{i}=\sum _{{j\in J}}{\frac {-a_{j}}{A}}x_{j},

where

A=\sum _{{i\in I}}a_{i}=-\sum _{{j\in J}}a_{j}.

The left hand side of the formula for p expresses this point as a convex combination of the points in I, and the right hand side expresses it as a convex combination of the points in J. Therefore, p belongs to both convex hulls, completing the proof.

This proof method allows for the efficient construction of a Radon point, in an amount of time that is polynomial in the dimension, by using Gaussian elimination or other efficient algorithms to solve the system of equations for the multipliers.[1]

Topological Radon theorem

A topological generalization of Radon's theorem states that, if ƒ is any continuous function from a (d + 1)-dimensional simplex to d-dimensional space, then the simplex has two disjoint faces whose images under ƒ are not disjoint.[2] Radon's theorem itself can be interpreted as the special case in which ƒ is the unique affine map that takes the vertices of the simplex to a given set of d + 2 points in d-dimensional space.

More generally, if K is any (d + 1)-dimensional compact convex set, and ƒ is any continuous function from K to d-dimensional space, then there exists a linear function g such that some point where g achieves its maximum value and some other point where g achieves its minimum value are mapped by ƒ to the same point. In the case where K is a simplex, the two simplex faces formed by the maximum and minimum points of g must then be two disjoint faces whose images have a nonempty intersection. This same general statement, when applied to a hypersphere instead of a simplex, gives the Borsuk–Ulam theorem, that ƒ must map two opposite points of the sphere to the same point.[2]

Applications

Radon's theorem forms a key step of a standard proof of Helly's theorem on intersections of convex sets;[3] this proof was the motivation for Radon's original discovery of Radon's theorem.

Radon's theorem can also be used to calculate the VC dimension of d-dimensional points with respect to linear separations. There exist sets of d + 1 points (for instance, the points of a regular simplex) such that every two nonempty subsets can be separated from each other by a hyperplane. However, no matter which set of d + 2 points is given, the two subsets of a Radon partition cannot be linearly separated. Therefore, the VC dimension of this system is exactly d + 1.[4]

A randomized algorithm that repeatedly replaces sets of d + 2 points by their Radon point can be used to compute an approximation to a centerpoint of any point set, in an amount of time that is polynomial in both the number of points and the dimension.[1]

Related concepts

The Radon point of three points in a one-dimensional space is just their median. The geometric median of a set of points is the point minimizing the sum of distances to the points in the set; it generalizes the one-dimensional median and has been studied both from the point of view of facility location and robust statistics. For sets of four points in the plane, the geometric median coincides with the Radon point.

Another generalization for partition into r sets was given by Helge Tverberg (1966) and is now known as Tverberg's theorem. It states that for any set of

(d+1)(r-1)+1\

points in Euclidean d-space, there is a partition into r subsets whose convex hulls intersect in at least one common point.

Carathéodory's theorem states that any point in the convex hull of some set of points is also within the convex hull of a subset of at most d + 1 of the points; that is, that the given point is part of a Radon partition in which it is a singleton. One proof of Carathéodory's theorem uses a technique of examining solutions to systems of linear equations, similar to the proof of Radon's theorem, to eliminate one point at a time until at most d + 1 remain.

Concepts related to Radon's theorem have also been considered for convex geometries, families of finite sets with the properties that the intersection of any two sets in the family remains in the family, and that the empty set and the union of all the sets belongs to the family. In this more general context, the convex hull of a set S is the intersection of the family members that contain S, and the Radon number of a space is the smallest r such that any r points have two subsets whose convex hulls intersect. Similarly, one can define the Helly number h and the Carathéodory number c by analogy to their definitions for convex sets in Euclidean spaces, and it can be shown that these numbers satisfy the inequalities h < r ≤ ch + 1.[5]

In an arbitrary undirected graph, one may define a convex set to be a set of vertices that includes every induced path connecting a pair of vertices in the set. With this definition, every set of ω + 1 vertices in the graph can be partitioned into two subsets whose convex hulls intersect, and ω + 1 is the minimum number for which this is possible, where ω is the clique number of the given graph.[6] For related results involving shortest paths instead of induced paths see Chepoi (1986) and Bandelt & Pesch (1989).

Notes

  1. ↑ 1.0 1.1 Clarkson et al. (1996).
  2. ↑ 2.0 2.1 Bajmóczy & Bárány (1979); Matoušek (2003).
  3. ↑ Matoušek (2002), p. 11.
  4. ↑ Epsilon-nets and VC-dimension, Lecture Notes by Marco Pellegrini, 2004.
  5. ↑ Kay & Womble (1971).
  6. ↑ Duchet (1987).

References

This article is issued from Wikipedia. The text is available under the Creative Commons Attribution/Share Alike; additional terms may apply for the media files.