Rademacher distribution
| Support | 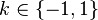 |
|---|---|
| pmf | 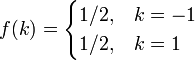 |
| CDF |  |
| Mean |  |
| Median |  |
| Mode | N/A |
| Variance |  |
| Skewness |  |
| Ex. kurtosis | 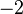 |
| Entropy |  |
| MGF | 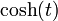 |
| CF | 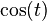 |
In probability theory and statistics, the Rademacher distribution (which is named after Hans Rademacher) is a discrete probability distribution where a random variate X has a 50% chance of being either +1 or -1.[1]
A series of Rademacher distributed variables can be regarded as a simple symmetrical random walk where the step size is 1.
Mathematical formulation
The probability mass function of this distribution is
It can be also written as a probability density function, in terms of the Dirac delta function, as
van Zuijlen's bound
van Zuijlen has proved the following result.[2]
Let Xi be a set of independent Rademacher distributed random variables. Then
The bound is sharp and better than that which can be derived from the normal distribution (approximately Pr > 0.31).
Bounds on sums
Let { Xi } be a set of random variables with a Rademacher distribution. Let { ai } be a sequence of real numbers. Then
where ||ai||2 is the Euclidean norm of the sequence { ai }, t is a real number > 0 and Pr(Z) is the probability of event Z.[3]
Also if ||ai||1 is finite then
where || ai ||1 is the 1-norm of the sequence { ai }.
Let Y = Σ Xiai and let Y be an almost surely convergent series in a Banach space. The for t > 0 and s ≥ 1 we have[4]
for some constant c.
Let p be a positive real number. Then[5]
where c1 and c2 are constants dependent only on p.
For p ≥ 1

Applications
The Rademacher distribution has been used in bootstrapping.
The Rademacher distribution can be used to show that normally distributed and uncorrelated does not imply independent.
Related distributions
- Bernoulli distribution: If X has a Rademacher distribution then
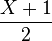 has a Bernoulli(1/2) distribution.
has a Bernoulli(1/2) distribution.
References
- ↑ Hitczenko P, Kwapień S (1994) On the Rademacher series. Progress in probability 35: 31-36
- ↑ van Zuijlen Martien CA (2011) On a conjecture concerning the sum of independent Rademacher random variables. http://arxiv.org/abs/1112.4988
- ↑ MontgomerySmith SJ (1990) The distribution of Rademacher sums. Proc Amer Math Soc 109: 517522
- ↑ Dilworth SJ, Montgomery-Smith SJ (1993) The distribution of vector-valued Radmacher series. Ann Probab 21 (4) 2046-2052
- ↑ Khintchine A (1923) Über dyadische Brüche. Math Zeitschr 18: 109–116
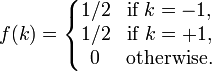
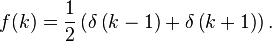

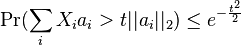

![Pr(||Y||>st)\leq [{\frac {1}{c}}Pr(||Y||>t)]^{{cs^{2}}}](/2014-wikipedia_en_all_02_2014/I/media/9/2/0/2/920225607e0592813e579d54044d0dd8.png)
![c_{1}[\sum {|a_{i}|^{2}}]^{{\frac {1}{2}}}\leq (E[|\sum {a_{i}X_{i}}|^{p}])^{{{\frac {1}{p}}}}\leq c_{2}[\sum {|a_{i}|^{2}}]^{{\frac {1}{2}}}](/2014-wikipedia_en_all_02_2014/I/media/4/a/7/7/4a77d19662f5f482ec5913eaa8d92b54.png)