R-tree
| R-tree | ||
|---|---|---|
| Type | Tree | |
| Invented | 1984 | |
| Invented by | Antonin Guttman | |
| Time complexity in big O notation | ||
| Average | Worst case | |
| Space | ||
| Search | O(logMn) | |
| Insert | O(n) | |
| Delete | ||

R-trees are tree data structures used for spatial access methods, i.e., for indexing multi-dimensional information such as geographical coordinates, rectangles or polygons. The R-tree was proposed by Antonin Guttman in 1984[1] and has found significant use in both theoretical and applied contexts.[2] A common real-world usage for an R-tree might be to store spatial objects such as restaurant locations or the polygons that typical maps are made of: streets, buildings, outlines of lakes, coastlines, etc. and then find answers quickly to queries such as "Find all museums within 2 km of my current location", "retrieve all road segments within 2 km of my location" (to display them in a navigation system) or "find the nearest gas station" (although not taking roads into account).
R-tree idea
The key idea of the data structure is to group nearby objects and represent them with their minimum bounding rectangle in the next higher level of the tree; the "R" in R-tree is for rectangle. Since all objects lie within this bounding rectangle, a query that does not intersect the bounding rectangle also cannot intersect any of the contained objects. At the leaf level, each rectangle describes a single object; at higher levels the aggregation of an increasing number of objects. This can also be seen as an increasingly coarse approximation of the data set.
Similar to the B-tree, the R-tree is also a balanced search tree (so all leaf nodes are at the same height), organizes the data in pages, and is designed for storage on disk (as used in databases). Each page can contain a maximum number of entries, often denoted as  . It also guarantees a minimum fill (except for the root node), however best performance has been experienced with a minimum fill of 30%–40% of the maximum number of entries (B-trees guarantee 50% page fill, and B*-trees even 66%). The reason for this is the more complex balancing required for spatial data as opposed to linear data stored in B-trees.
. It also guarantees a minimum fill (except for the root node), however best performance has been experienced with a minimum fill of 30%–40% of the maximum number of entries (B-trees guarantee 50% page fill, and B*-trees even 66%). The reason for this is the more complex balancing required for spatial data as opposed to linear data stored in B-trees.
As with most trees, the searching algorithms (e.g., intersection, containment, nearest neighbor search) are rather simple. The key idea is to use the bounding boxes to decide whether or not to search inside a subtree. In this way, most of the nodes in the tree are never read during a search. Like B-trees, this makes R-trees suitable for large data sets and databases, where nodes can be paged to memory when needed, and the whole tree cannot be kept in main memory.
The key difficulty of R-trees is to build an efficient tree that on one hand is balanced (so the leaf nodes are at the same height) on the other hand the rectangles do not cover too much empty space and do not overlap too much (so that during search, fewer subtrees need to be processed). For example, the original idea for inserting elements to obtain an efficient tree is to always insert into the subtree that requires least enlargement of its bounding box. Once that page is full, the data is split into two sets that should cover the minimal area each. Most of the research and improvements for R-trees aims at improving the way the tree is built and can be grouped into two objectives: building an efficient tree from scratch (known as bulk-loading) and performing changes on an existing tree (insertion and deletion).
R-trees do not guarantee good worst-case performance, but generally perform well with real-world data.[3] While more of theoretical interest, the (bulk-loaded) Priority R-tree variant of the R-tree is worst-case optimal,[4] but due to the increased complexity, has not received much attention in practical applications so far.
When data is organized in an R-tree, the k nearest neighbors (for any Lp-Norm) of all points can efficiently be computed using a spatial join.[5] This is beneficial for many algorithms based on the k nearest neighbors, for example the Local Outlier Factor. DeLi-Clu,[6] Density-Link-Clustering is a cluster analysis algorithm that uses the R-tree structure for a similar kind of spatial join to efficiently compute an OPTICS clustering.
Variants
Algorithm
Data layout
Data in R-trees is organized in pages, that can have a variable number of entries (up to some pre-defined maximum, and usually above a minimum fill). Each entry within a non-leaf node stores two pieces of data: a way of identifying a child node, and the bounding box of all entries within this child node. Leaf nodes store the data required for each child, often a point or bounding box representing the child and an external identifier for the child. For point data, the leaf entries can be just the points themselves. For polygon data (that often requires the storage of large polygons) the common setup is to store only the MBR (minimum bounding rectangle) of the polygon along with a unique identifier in the tree.
Search
The input is a search rectangle (Query box). Searching is quite similar to searching in a B+ tree. The search starts from the root node of the tree. Every internal node contains a set of rectangles and pointers to the corresponding child node and every leaf node contains the rectangles of spatial objects (the pointer to some spatial object can be there). For every rectangle in a node, it has to be decided if it overlaps the search rectangle or not. If yes, the corresponding child node has to be searched also. Searching is done like this in a recursive manner until all overlapping nodes have been traversed. When a leaf node is reached, the contained bounding boxes (rectangles) are tested against the search rectangle and their objects (if there are any) are put into the result set if they lie within the search rectangle.
Insertion
To insert an object, the tree is traversed recursively from the root node. At each step, all rectangles in the current directory node are examined, and a candidate is chosen using a heuristic such as choosing the rectangle which requires least enlargement. The search then descends into this page, until reaching a leaf node. If the leaf node is full, it must be split before the insertion is made. Again, since an exhaustive search is too expensive, a heuristic is employed to split the node into two. Adding the newly created node to the previous level, this level can again overflow, and these overflows can propagate up to the root node; when this node also overflows, a new root node is created and the tree has increased in height.
Choosing the insertion subtree
At each level, the algorithm needs to decide in which subtree to insert the new data object. When a data object is fully contained in a single rectangle, the choice is clear. When there are multiple options or rectangles in need of enlargement, the choice can have a significant impact on the performance of the tree.
In the classic R-tree, objects are inserted into the subtree that needs the least enlargement. In the more advanced R*-tree, a mixed heuristic is employed. At leaf level, it tries to minimize the overlap (in case of ties, prefer least enlargement and then least area); at the higher levels, it behaves similar to the R-tree, but on ties again preferring the subtree with smaller area. The decreased overlap of rectangles in the R*-tree is one of the key benefits over the traditional R-tree (this is also a consequence of the other heuristics used, not only the subtree choosing).
Splitting an overflowing node
Since redistributing all objects of a node into two nodes has an exponential number of options, a heuristic needs to be employed to find the best split. In the classic R-tree, Guttman proposed two such heuristics, called QuadraticSplit and LinearSplit. In quadratic split, the algorithm searches the pair of rectangles that is the worst combination to have in the same node, and puts them as initial objects into the two new groups. It then searches the entry which has the strongest preference for one of the groups (in terms of area increase) and assigns the object to this group until all objects are assigned (satisfying the minimum fill).
There are other splitting strategies such as Greene's Split,[7] the R*-tree splitting heuristic[8] (which again tries to minimize overlap, but also prefers quadratic pages) or the linear split algorithm proposed by Ang and Tan[9] (which however can produce very unregular rectangles, which are less performant for many real world range and window queries). In addition to having a more advanced splitting heuristic, the R*-tree also tries to avoid splitting a node by reinserting some of the node members, which is similar to the way a B-tree balances overflowing nodes. This was shown to also reduce overlap and thus increase tree performance.
Finally, the X-tree[10] can be seen as a R*-tree variant that can also decide to not split a node, but construct a so-called super-node containing all the extra entries, when it doesn't find a good split (in particular for high-dimensional data).
| Effect of different splitting heuristics on a database with Germany postal districts | |||||||||
|---|---|---|---|---|---|---|---|---|---|
| |||||||||
Deletion
Deleting an entry from a page may require updating the bounding rectangles of parent pages. However, when a page is underfull, it will not be balanced with its neighbors. Instead, the page will be dissolved and all its children (which may be subtrees, not only leaf objects) will be reinserted. If during this process the root node has a single element, the tree height can decrease.
Bulk-loading
- Nearest-X - Objects are sorted by their first coordinate ("X") and then split into pages of the desired size.
- Packed Hilbert R-tree - variation of Nearest-X, but sorting using the Hilbert value of the center of a rectangle instead of using the X coordinate. There is no guarantee the pages will not overlap.
- Sort-Tile-Recursive (STR):[11] Another variation of Nearest-X, that estimates the total number of leaves required as
 , the required split factor in each dimension to achieve this as
, the required split factor in each dimension to achieve this as 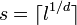 , then repeatedly splits each dimensions successively into
, then repeatedly splits each dimensions successively into  equal sized partitions using 1-dimensional sorting. The resulting pages, if they occupy more than one page, are again bulk-loaded using the same algorithm. For point data, the leaf nodes will not overlap, and "tile" the data space into approximately equal sized pages.
equal sized partitions using 1-dimensional sorting. The resulting pages, if they occupy more than one page, are again bulk-loaded using the same algorithm. For point data, the leaf nodes will not overlap, and "tile" the data space into approximately equal sized pages. - Priority R-tree
See also
- Segment tree
- Interval tree - A degenerate R-tree for one dimension (usually time).
- Bounding volume hierarchy
- Spatial index
- GiST
References
- ↑ 1.0 1.1 1.2 Guttman, A. (1984). "R-Trees: A Dynamic Index Structure for Spatial Searching". Proceedings of the 1984 ACM SIGMOD international conference on Management of data - SIGMOD '84. p. 47. doi:10.1145/602259.602266. ISBN 0897911288.
- ↑ Y. Manolopoulos; A. Nanopoulos; Y. Theodoridis (2006). R-Trees: Theory and Applications. Springer. ISBN 978-1-85233-977-7. Retrieved 8 October 2011.
- ↑ Hwang, S.; Kwon, K.; Cha, S. K.; Lee, B. S. (2003). "Performance Evaluation of Main-Memory R-tree Variants". Advances in Spatial and Temporal Databases. Lecture Notes in Computer Science 2750. p. 10. doi:10.1007/978-3-540-45072-6_2. ISBN 978-3-540-40535-1.
- ↑ Arge, L.; De Berg, M.; Haverkort, H. J.; Yi, K. (2004). "The Priority R-tree". Proceedings of the 2004 ACM SIGMOD international conference on Management of data - SIGMOD '04. p. 347. doi:10.1145/1007568.1007608. ISBN 1581138598.
- ↑ Brinkhoff, T.; Kriegel, H. P.; Seeger, B. (1993). "Efficient processing of spatial joins using R-trees". ACM SIGMOD Record 22 (2): 237. doi:10.1145/170036.170075.
- ↑ Achtert, E.; Böhm, C.; Kröger, P. (2006). "DeLi-Clu: Boosting Robustness, Completeness, Usability, and Efficiency of Hierarchical Clustering by a Closest Pair Ranking". LNCS: Advances in Knowledge Discovery and Data Mining. Lecture Notes in Computer Science 3918: 119–128. doi:10.1007/11731139_16. ISBN 978-3-540-33206-0.
- ↑ Greene, D. (1989). "An implementation and performance analysis of spatial data access methods". [1989] Proceedings. Fifth International Conference on Data Engineering. pp. 606–615. doi:10.1109/ICDE.1989.47268. ISBN 0-8186-1915-5.
- ↑ 8.0 8.1 8.2 Beckmann, N.; Kriegel, H. P.; Schneider, R.; Seeger, B. (1990). "The R*-tree: an efficient and robust access method for points and rectangles". Proceedings of the 1990 ACM SIGMOD international conference on Management of data - SIGMOD '90. p. 322. doi:10.1145/93597.98741. ISBN 0897913655.
- ↑ 9.0 9.1 9.2 Ang, C. H.; Tan, T. C. (1997). "New linear node splitting algorithm for R-trees". In Scholl, Michel; Voisard, Agnès. Proceedings of the 5th International Symposium on Advances in Spatial Databases (SSD '97), Berlin, Germany, July 15–18, 1997. Lecture Notes in Computer Science 1262. Springer. pp. 337–349. doi:10.1007/3-540-63238-7_38.
- ↑ Berchtold, Stefan; Keim, Daniel A.; Kriegel, Hans-Peter (1996). "The X-Tree: An Index Structure for High-Dimensional Data". Proceedings of the 22nd VLDB Conference (Mumbai, India): 28–39.
- ↑ Leutenegger, Scott T.; Edgington, Jeffrey M.; Lopez, Mario A. (February 1997). STR: A Simple and Efficient Algorithm for R-Tree Packing.
External links
| Wikimedia Commons has media related to R-tree. |
- R-tree portal
- R-tree implementations: C & C++, Java applet, Common Lisp, Python, Javascript, Javascript AMD module
- Boost.Geometry library containing R-tree implementation (various splitting algorithms)
| ||||||||||||||||||||||||||
| |||||||||||||||||||||||


