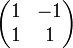Quincunx matrix

From Wikipedia, the free encyclopedia

In mathematics, the matrix

{\begin{pmatrix}1&-1\\1&1\end{pmatrix}}

is sometimes called the quincunx matrix. It is a 2×2 Hadamard matrix, and its rows form the basis of a diagonal square lattice consisting of the integer points whose coordinates both have the same parity; this lattice is a two-dimensional analogue of the three-dimensional body-centered cubic lattice.[1]

See also

Notes

  1. ↑ Van De Ville, D.; Blu, T.; Unser, M. (2005), "On the multidimensional extension of the quincunx subsampling matrix", IEEE Signal Processing Letters 12 (2): 112–115, doi:10.1109/LSP.2004.839697 .


This article is issued from Wikipedia. The text is available under the Creative Commons Attribution/Share Alike; additional terms may apply for the media files.