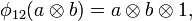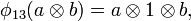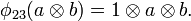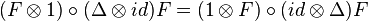Quasitriangular Hopf algebra

From Wikipedia, the free encyclopedia

In mathematics, a Hopf algebra, H, is quasitriangular[1] if there exists an invertible element, R, of 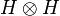H\otimes H such that

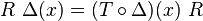  • R\ \Delta (x)=(T\circ \Delta )(x)\ R for all x\in H, where \Delta is the coproduct on H, and the linear map T:H\otimes H\to H\otimes H is given by T(x\otimes y)=y\otimes x,
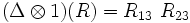  • (\Delta \otimes 1)(R)=R_{{13}}\ R_{{23}},
  • (1\otimes \Delta )(R)=R_{{13}}\ R_{{12}},

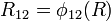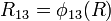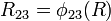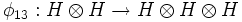where R_{{12}}=\phi _{{12}}(R), R_{{13}}=\phi _{{13}}(R), and R_{{23}}=\phi _{{23}}(R), where \phi _{{12}}:H\otimes H\to H\otimes H\otimes H, \phi _{{13}}:H\otimes H\to H\otimes H\otimes H, and \phi _{{23}}:H\otimes H\to H\otimes H\otimes H, are algebra morphisms determined by

\phi _{{12}}(a\otimes b)=a\otimes b\otimes 1,
\phi _{{13}}(a\otimes b)=a\otimes 1\otimes b,
\phi _{{23}}(a\otimes b)=1\otimes a\otimes b.

R is called the R-matrix.

As a consequence of the properties of quasitriangularity, the R-matrix, R, is a solution of the Yang-Baxter equation (and so a module V of H can be used to determine quasi-invariants of braids, knots and links). Also as a consequence of the properties of quasitriangularity, 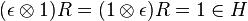(\epsilon \otimes 1)R=(1\otimes \epsilon )R=1\in H; moreover 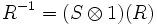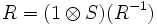R^{{-1}}=(S\otimes 1)(R), R=(1\otimes S)(R^{{-1}}), and (S\otimes S)(R)=R. One may further show that the antipode S must be a linear isomorphism, and thus S^2 is an automorphism. 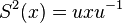In fact, S^2 is given by conjugating by an invertible element: S^{2}(x)=uxu^{{-1}} where u:=m(S\otimes 1)R^{{21}} (cf. Ribbon Hopf algebras).

It is possible to construct a quasitriangular Hopf algebra from a Hopf algebra and its dual, using the Drinfeld quantum double construction.

Twisting

The property of being a quasi-triangular Hopf algebra is preserved by twisting via an invertible element 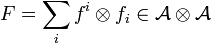F=\sum _{i}f^{i}\otimes f_{i}\in {\mathcal {A\otimes A}} such that 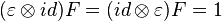(\varepsilon \otimes id)F=(id\otimes \varepsilon )F=1 and satisfying the cocycle condition

(F\otimes 1)\circ (\Delta \otimes id)F=(1\otimes F)\circ (id\otimes \Delta )F

Furthermore, 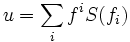u=\sum _{i}f^{i}S(f_{i}) is invertible and the twisted antipode is given by 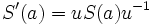S'(a)=uS(a)u^{{-1}}, with the twisted comultiplication, R-matrix and co-unit change according to those defined for the quasi-triangular Quasi-Hopf algebra. Such a twist is known as an admissible (or Drinfeld) twist.

See also

Notes

  1. ↑ Montgomery & Schneider (2002), p. 72.

References

This article is issued from Wikipedia. The text is available under the Creative Commons Attribution/Share Alike; additional terms may apply for the media files.