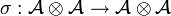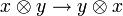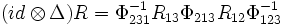Quasi-triangular Quasi-Hopf algebra

From Wikipedia, the free encyclopedia

A quasi-triangular quasi-Hopf algebra is a specialized form of a quasi-Hopf algebra defined by the Ukrainian mathematician Vladimir Drinfeld in 1989. It is also a generalized form of a quasi-triangular Hopf algebra.

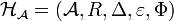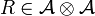A quasi-triangular quasi-Hopf algebra is a set {\mathcal {H_{A}}}=({\mathcal {A}},R,\Delta ,\varepsilon ,\Phi ) where {\mathcal {B_{A}}}=({\mathcal {A}},\Delta ,\varepsilon ,\Phi ) is a quasi-Hopf algebra and R\in {\mathcal {A\otimes A}} known as the R-matrix, is an invertible element such that

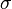R\Delta (a)=\sigma \circ \Delta (a)R,a\in {\mathcal {A}}
\sigma :{\mathcal {A\otimes A}}\rightarrow {\mathcal {A\otimes A}}
x\otimes y\rightarrow y\otimes x

so that \sigma is the switch map and

(\Delta \otimes id)R=\Phi _{{321}}R_{{13}}\Phi _{{132}}^{{-1}}R_{{23}}\Phi _{{123}}
(id\otimes \Delta )R=\Phi _{{231}}^{{-1}}R_{{13}}\Phi _{{213}}R_{{12}}\Phi _{{123}}^{{-1}}

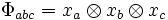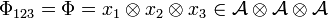where \Phi _{{abc}}=x_{a}\otimes x_{b}\otimes x_{c} and \Phi _{{123}}=\Phi =x_{1}\otimes x_{2}\otimes x_{3}\in {\mathcal {A\otimes A\otimes A}}.

The quasi-Hopf algebra becomes triangular if in addition, 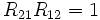R_{{21}}R_{{12}}=1.

The twisting of 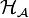{\mathcal {H_{A}}} by F\in {\mathcal {A\otimes A}} is the same as for a quasi-Hopf algebra, with the additional definition of the twisted R-matrix

A quasi-triangular (resp. triangular) quasi-Hopf algebra with 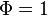\Phi =1 is a quasi-triangular (resp. triangular) Hopf algebra as the latter two conditions in the definition reduce the conditions of quasi-triangularity of a Hopf algebra .

Similarly to the twisting properties of the quasi-Hopf algebra, the property of being quasi-triangular or triangular quasi-Hopf algebra is preserved by twisting.

See also

References

  • Vladimir Drinfeld, Quasi-Hopf algebras, Leningrad Math J. 1 (1989), 1419-1457
  • J.M. Maillet and J. Sanchez de Santos, Drinfeld Twists and Algebraic Bethe Ansatz, Amer. Math. Soc. Transl. (2) Vol. 201, 2000
This article is issued from Wikipedia. The text is available under the Creative Commons Attribution/Share Alike; additional terms may apply for the media files.