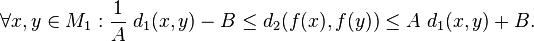Quasi-isometry
In mathematics, quasi-isometry is an equivalence relation on metric spaces that ignores their small-scale details in favor of their coarse structure. The concept is especially important in Gromov's geometric group theory.

Definition
Suppose that  is a (not necessarily continuous) function from one metric space
is a (not necessarily continuous) function from one metric space 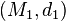 to a second metric space
to a second metric space  . Then
. Then  is called a quasi-isometry from
is called a quasi-isometry from 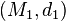 to
to  if there exist constants
if there exist constants  ,
, 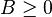 , and
, and  such that the following two properties both hold:
such that the following two properties both hold:
- For every two points
 and
and  in
in  , the distance between their images is (up to the additive constant
, the distance between their images is (up to the additive constant  ) within a factor of
) within a factor of  of their original distance. More formally:
of their original distance. More formally:
- Every point of
 is within the constant distance
is within the constant distance  of an image point. More formally:
of an image point. More formally:
The two metric spaces 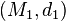 and
and  are called quasi-isometric if there exists a quasi-isometry
are called quasi-isometric if there exists a quasi-isometry  from
from 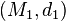 to
to  .
.
Examples
The map between the Euclidean plane and the plane with the Manhattan distance that sends every point to itself is a quasi-isometry: in it, distances are multiplied by a factor of at most  .
.
The map 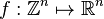 (both with the Euclidean metric) that sends every
(both with the Euclidean metric) that sends every  -tuple of integers to itself is a quasi-isometry: distances are preserved exactly, and every real tuple is within distance
-tuple of integers to itself is a quasi-isometry: distances are preserved exactly, and every real tuple is within distance 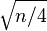 of an integer tuple. In the other direction, the discontinuous function that rounds every tuple of real numbers to the nearest integer tuple is also a quasi-isometry: each point is taken by this map to a point within distance
of an integer tuple. In the other direction, the discontinuous function that rounds every tuple of real numbers to the nearest integer tuple is also a quasi-isometry: each point is taken by this map to a point within distance 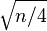 of it, so rounding changes the distance between pairs of points by adding or subtracting at most
of it, so rounding changes the distance between pairs of points by adding or subtracting at most 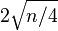 .
.
Every pair of finite or bounded metric spaces is quasi-isometric. In this case, every function from one space to the other is a quasi-isometry.
Equivalence relation
If 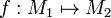 is a quasi-isometry, then there exists a quasi-isometry
is a quasi-isometry, then there exists a quasi-isometry 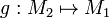 . Indeed,
. Indeed, 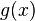 may be defined by letting
may be defined by letting  be any point in the image of
be any point in the image of  that is within distance
that is within distance  of
of  , and letting
, and letting 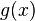 be any point in
be any point in 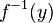 .
.
Since the identity map is a quasi-isometry, and the composition of two quasi-isometries is a quasi-isometry, it follows that the relation of being quasi-isometric is an equivalence relation on the class of metric spaces.
Use in geometric group theory
Given a finite generating set S of a finitely generated group G, we can form the corresponding Cayley graph of S and G. This graph becomes a metric space if we declare the length of each edge to be 1. Taking a different finite generating set T results in a different graph and a different metric space, however the two spaces are quasi-isometric. This quasi-isometry class is thus an invariant of the group G. Any property of metric spaces that only depends on a space's quasi-isometry class immediately yields another invariant of groups, opening the field of group theory to geometric methods.
References
- Bridson, Martin R. (2008), "Geometric and combinatorial group theory", in Gowers, Timothy; Barrow-Green, June; Leader, Imre, The Princeton Companion to Mathematics, Princeton University Press, pp. 431–448, ISBN 978-0-691-11880-2