Quasi-compact morphism

In algebraic geometry, a morphism between schemes is said to be quasi-compact if Y can be covered by open affine subschemes such that the pre-images 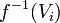are quasi-compact (as topological space).^[1] If f is quasi-compact, then the pre-image of a quasi-compact open subscheme (e.g., open affine subscheme) under f is quasi-compact.

It is not enough that Y admits a covering by quasi-compact open subschemes whose pre-images are quasi-compact. To give an example,^[2] let A be a ring that does not satisfy the ascending chain conditions on radical ideals, and put 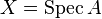. X contains an open subset U that is not quasi-compact. Let Y be the scheme obtained by gluing two X's along U. X, Y are both quasi-compact. If is the inclusion of one of the copies of X, then the pre-image of the other X, open affine in Y, is U, not quasi-compact. Hence, f is not quasi-compact.

A morphism from a quasi-compact scheme to an affine scheme is quasi-compact.

Let be a quasi-compact morphism between schemes. Then 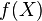is closed if and only if it is stable under specialization.

The composition of quasi-compact morphisms is quasi-compact. The base change of a quasi-compact morphism is quasi-compact.

An affine scheme is quasi-compact. In fact, a scheme is quasi-compact if and only if it is a finite union of open affine subschemes. Serre’s criterion gives a necessary and sufficient condition for a quasi-compact scheme to be affine.

A quasi-compact scheme has at least one closed point.^{[citation needed]}

See also

• fpqc morphism

External links

• http://mathoverflow.net/questions/34620/when-is-an-irreducible-scheme-quasi-compact

References

• Hartshorne, Algebraic Geometry.
• Angelo Vistoli, "Notes on Grothendieck topologies, fibered categories and descent theory." arXiv:math.AG/0412512v4