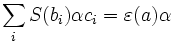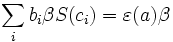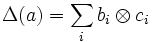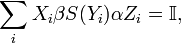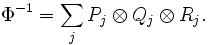Quasi-Hopf algebra

From Wikipedia, the free encyclopedia

A quasi-Hopf algebra is a generalization of a Hopf algebra, which was defined by the Russian mathematician Vladimir Drinfeld in 1989.

A quasi-Hopf algebra is a quasi-bialgebra {\mathcal {B_{A}}}=({\mathcal {A}},\Delta ,\varepsilon ,\Phi )for which there exist 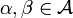\alpha ,\beta \in {\mathcal {A}} and a bijective antihomomorphism S (antipode) of {\mathcal {A}} such that

\sum _{i}S(b_{i})\alpha c_{i}=\varepsilon (a)\alpha
\sum _{i}b_{i}\beta S(c_{i})=\varepsilon (a)\beta

for all a\in {\mathcal {A}} and where

\Delta (a)=\sum _{i}b_{i}\otimes c_{i}

and

\sum _{i}X_{i}\beta S(Y_{i})\alpha Z_{i}={\mathbb {I}},
\sum _{j}S(P_{j})\alpha Q_{j}\beta S(R_{j})={\mathbb {I}}.

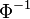where the expansions for the quantities \Phi and \Phi ^{{-1}} are given by

\Phi =\sum _{i}X_{i}\otimes Y_{i}\otimes Z_{i}

and

\Phi ^{{-1}}=\sum _{j}P_{j}\otimes Q_{j}\otimes R_{j}.

As for a quasi-bialgebra, the property of being quasi-Hopf is preserved under twisting.

Usage

Quasi-Hopf algebras form the basis of the study of Drinfeld twists and the representations in terms of F-matrices associated with finite-dimensional irreducible representations of quantum affine algebra. F-matrices can be used to factorize the corresponding R-matrix. This leads to applications in Statistical mechanics, as quantum affine algebras, and their representations give rise to solutions of the Yang-Baxter equation, a solvability condition for various statistical models, allowing characteristics of the model to be deduced from its corresponding quantum affine algebra. The study of F-matrices has been applied to models such as the Heisenberg XXZ model in the framework of the algebraic Bethe ansatz. It provides a framework for solving two-dimensional integrable models by using the Quantum inverse scattering method.

See also

References

  • Vladimir Drinfeld, Quasi-Hopf algebras, Leningrad Math J. 1 (1989), 1419-1457
  • J.M. Maillet and J. Sanchez de Santos, Drinfeld Twists and Algebraic Bethe Ansatz, Amer. Math. Soc. Transl. (2) Vol. 201, 2000
This article is issued from Wikipedia. The text is available under the Creative Commons Attribution/Share Alike; additional terms may apply for the media files.