Quarter cubic honeycomb

From Wikipedia, the free encyclopedia
Quarter cubic honeycomb
 
TypeUniform honeycomb
FamilyTruncated simplectic honeycomb
Quarter hypercubic honeycomb
Indexing[1] J25,33, A13
W10, G6
Schläfli symbolt0,1{3[4]} or q{4,3,4}
Coxeter-Dynkin diagram =
Cell types{3,3}
(3.6.6)
Face types{3}, {6}
Vertex figure
(elongated triangular antiprism)
Cells/vertex(3.6.6)6+{3,3}2
Space groupFd3m (227)
Coxeter group{{\tilde {A}}}_{3}×2, [[3[4]]] (double)
Dualoblate cubille
(Trigonal trapezohedral honeycomb)
Propertiesvertex-transitive, edge-transitive

The quarter cubic honeycomb (or bitruncated alternated cubic honeycomb) is a space-filling tessellation (or honeycomb) in Euclidean 3-space. It is composed of tetrahedra and truncated tetrahedra in a ratio of 1:1. It is called "quarter-cubic" because its symmetry unit – the minimal block from which the pattern is developed by reflections – consists of four such units of the cubic honeycomb.

It is vertex-transitive with 6 truncated tetrahedra and 2 tetrahedra around each vertex.

It is one of the 28 convex uniform honeycombs.

The faces of this honeycomb's cells form four families of parallel planes, each with a 3.6.3.6 tiling.

Its vertex figure is an isosceles antiprism: two equilateral triangles joined by six isosceles triangles.

John Horton Conway calls this honeycomb a truncated tetrahedrille, and its dual oblate cubille.

Construction

The quarter cubic honeycomb can be constructed in slab layers of truncated tetrahedra and tetrahedral cells, seen as two trihexagonal tilings. Two tetrahedra are stacked by a vertex and a central inversion. In each trihexagonal tiling, half of the triangles belong to tetrahedra, and half belong to truncated tetrahedra. These slab layers must be stacked with tetrahedra triangles to truncated tetrahedral triangles to construct the uniform quarter cubic honeycomb. Slab layers of hexagonal prisms and triangular prisms can be alternated for elongated honeycombs, but these are also not uniform.


trihexagonal tiling:

Symmetry

Cells can be shown in two different symmetries. The reflection generated form represented by its Coxeter-Dynkin diagram has two colors of truncated cuboctahedra. The symmetry can be doubled by relating the pairs of ringed and unringed nodes of the Coxeter-Dynkin diagram, which can been shown with one colored tetrahedral and truncated tetrahedral cells.

Two uniform colorings
Symmetry {{\tilde {A}}}_{3}, [3[4]] {{\tilde {A}}}_{3}×2, [[3[4]]]
Space group F43m (216) Fd3m (227)
Coloring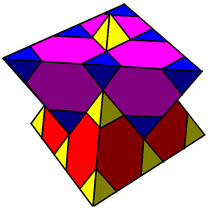
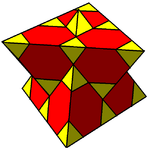Vertex figure
Vertex
figure
symmetry		 C3v
[3]
(*33)
order 6		 D3d
[2+,6]
(2*3)
order 12

Related polyhedra


The subset of hexagonal faces of thus honeycomb contains an infinite regular skew polyhedron {6,6|3}.
Four sets of parallel planes of trihexagonal tilings exist throughout this honeycomb.

This honeycomb is one of five distinct uniform honeycombs[2] constructed by the {{\tilde {A}}}_{3} Coxeter group. The symmetry can be multiplied by the symmetry of rings in the Coxeter–Dynkin diagrams:

Space
group		 Fibrifold Square
symmetry		 Extended
symmetry		 Extended
diagram		 Extended
order		 Honeycomb diagrams
F43m
(216)		 1o:2 a1 [3[4]] ×1 (None)
Fd3m
(227)		 2+:2 p2 [[3[4]]]
= 		×2  3
Fm3m
(225)		 2−:2 d2 <[3[4]]>
= [4,3,31,1]
= 		×2  1, 2
Pm3m
(221)		 4−:2 d4 [2[3[4]]]
= [4,3,4]
= 		×4  4
Im3m
(229)		 8o:2 r8 [4[3[4]]]
= [[4,3,4]]
= 		×8  5,  (*)
Space
group		 Fibrifold Extended
symmetry		 Extended
diagram		 Order Honeycombs
Pm3m
(221)		 4−:2 [4,3,4] ×1 1, 2, 3, 4,
5, 6
Fm3m
(225)		 2−:2 [1+,4,3,4]
= [4,31,1]
= 		Half 7, 11, 12, 13
I43m
(217)		 4o:2 [[(4,3,4,2+)]] Half × 2 (7),
Fd3m
(227)		 2+:2 [[1+,4,3,4,1+]]
= [[3[4]]]
= 		Quarter × 2 10,
Im3m
(229)		 8o:2 [[4,3,4]] ×2

(1), 8, 9

See also

Wikimedia Commons has media related to Quarter cubic honeycomb.

References

  1. ↑ For cross-referencing, they are given with list indices from Andreini (1-22), Williams(1-2,9-19), Johnson (11-19, 21-25, 31-34, 41-49, 51-52, 61-65), and Grünbaum(1-28).
  2. ↑ , A000029 6-1 cases, skipping one with zero marks
  • John H. Conway, Heidi Burgiel, Chaim Goodman-Strauss, (2008) The Symmetries of Things, ISBN 978-1-56881-220-5 (Chapter 21, Naming the Archimedean and Catalan polyhedra and tilings, Architectonic and Catoptric tessellations, p 292-298, includes all the nonprismatic forms)
  • George Olshevsky, Uniform Panoploid Tetracombs, Manuscript (2006) (Complete list of 11 convex uniform tilings, 28 convex uniform honeycombs, and 143 convex uniform tetracombs)
  • Branko Grünbaum, Uniform tilings of 3-space. Geombinatorics 4(1994), 49 - 56.
  • Norman Johnson Uniform Polytopes, Manuscript (1991)
  • Williams, Robert (1979). The Geometrical Foundation of Natural Structure: A Source Book of Design. Dover Publications, Inc. ISBN 0-486-23729-X. 
  • Critchlow, Keith (1970). Order in Space: A design source book. Viking Press. ISBN 0-500-34033-1. 
  • Kaleidoscopes: Selected Writings of H.S.M. Coxeter, edited by F. Arthur Sherk, Peter McMullen, Anthony C. Thompson, Asia Ivic Weiss, Wiley-Interscience Publication, 1995, ISBN 978-0-471-01003-6
    • (Paper 22) H.S.M. Coxeter, Regular and Semi Regular Polytopes I, [Math. Zeit. 46 (1940) 380-407, MR 2,10] (1.9 Uniform space-fillings)
  • A. Andreini, Sulle reti di poliedri regolari e semiregolari e sulle corrispondenti reti correlative (On the regular and semiregular nets of polyhedra and on the corresponding correlative nets), Mem. Società Italiana della Scienze, Ser.3, 14 (1905) 75–129.
  • D. M. Y. Sommerville, An Introduction to the Geometry of n Dimensions. New York, E. P. Dutton, 1930. 196 pp. (Dover Publications edition, 1958) Chapter X: The Regular Polytopes
  • Richard Klitzing, 3D Euclidean Honeycombs, x3x3o3o3*a - batatoh - O27
  • Uniform Honeycombs in 3-Space: 15-Batatoh
Fundamental convex regular and uniform honeycombs in dimensions 2–11
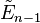Family {{\tilde {A}}}_{{n-1}} {{\tilde {C}}}_{{n-1}} {{\tilde {B}}}_{{n-1}} {{\tilde {D}}}_{{n-1}} {{\tilde {G}}}_{2} / {{\tilde {F}}}_{4} / {{\tilde {E}}}_{{n-1}}
Uniform tiling {3[3]} δ3 hδ3 qδ3 Hexagonal
Uniform convex honeycomb {3[4]} δ4 hδ4 qδ4
Uniform 5-honeycomb {3[5]} δ5 hδ5 qδ5 24-cell honeycomb
Uniform 6-honeycomb {3[6]} δ6 hδ6 qδ6
Uniform 7-honeycomb {3[7]} δ7 hδ7 qδ7 222
Uniform 8-honeycomb {3[8]} δ8 hδ8 qδ8 133 • 331
Uniform 9-honeycomb {3[9]} δ9 hδ9 qδ9 152 • 251 • 521
Uniform n-honeycomb {3[n]} δn hδn qδn 1k2 • 2k1 • k21
This article is issued from Wikipedia. The text is available under the Creative Commons Attribution/Share Alike; additional terms may apply for the media files.