Quarter 7-cubic honeycomb
From Wikipedia, the free encyclopedia
| quarter 7-cubic honeycomb | |
|---|---|
| (No image) | |
| Type | Uniform 7-honeycomb |
| Family | Quarter hypercubic honeycomb |
| Schläfli symbol | q{4,3,3,3,3,3,4} |
| Coxeter diagram | |
| 6-face type | h{4,35},  h5{4,35},  {31,1,1}×{3,3} duoprism |
| Vertex figure | |
| Coxeter group | 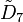 ×2 = [[31,1,3,3,3,31,1]] ×2 = [[31,1,3,3,3,31,1]] |
| Dual | |
| Properties | vertex-transitive |
In seven-dimensional Euclidean geometry, the quarter 7-cubic honeycomb is a uniform space-filling tessellation (or honeycomb). It has half the vertices of the 7-demicubic honeycomb, and a quarter of the vertices of a 7-cube honeycomb.[1] Its facets are 7-demicubes, pentellated 7-demicubes, and {31,1,1}×{3,3} duoprisms.
Related honeycombs
This honeycomb is one of 77 uniform honycombs constructed by the 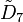 Coxeter group, all but 10 repeated in other families by extended symmetry, seen in the graph symmetry of rings in the Coxeter–Dynkin diagrams. The 77 permutations are listed with its highest extended symmetry, and related
Coxeter group, all but 10 repeated in other families by extended symmetry, seen in the graph symmetry of rings in the Coxeter–Dynkin diagrams. The 77 permutations are listed with its highest extended symmetry, and related 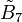 and
and  constructions:
constructions:
| Extended symmetry |
Extended diagram |
Order | Honeycombs |
|---|---|---|---|
| [31,1,3,3,3,31,1] | ×1 | ||
| [[31,1,3,3,3,31,1]] | ×2 | ||
| <[31,1,3,3,3,31,1]> = [31,1,3,3,3,3,4] |
= |
×2 | |
| <<[31,1,3,3,3,31,1]>> = [4,3,3,3,3,3,4] |
= |
×4 | |
| [<<[31,1,3,3,3,31,1]>>] = [[4,3,3,3,3,3,4]] |
= |
×8 |
See also
Regular and uniform honeycombs in 7-space:
- 7-cube honeycomb
- 7-demicube honeycomb
- 7-simplex honeycomb
- Truncated 7-simplex honeycomb
- Omnitruncated 7-simplex honeycomb
Notes
- ↑ Coxeter, Regular and Semi-Regular Polytopes III, (1988), p318
References
- Kaleidoscopes: Selected Writings of H.S.M. Coxeter, edited by F. Arthur Sherk, Peter McMullen, Anthony C. Thompson, Asia Ivic Weiss, Wiley-Interscience Publication, 1995, ISBN 978-0-471-01003-6
- Richard Klitzing, 7D, Euclidean tesselations#7D
| Fundamental convex regular and uniform honeycombs in dimensions 2–11 | |||||
|---|---|---|---|---|---|
| Family |  |
 |
 |
 |
 / /  / / 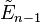 |
| Uniform tiling | {3[3]} | δ3 | hδ3 | qδ3 | Hexagonal |
| Uniform convex honeycomb | {3[4]} | δ4 | hδ4 | qδ4 | |
| Uniform 5-honeycomb | {3[5]} | δ5 | hδ5 | qδ5 | 24-cell honeycomb |
| Uniform 6-honeycomb | {3[6]} | δ6 | hδ6 | qδ6 | |
| Uniform 7-honeycomb | {3[7]} | δ7 | hδ7 | qδ7 | 222 |
| Uniform 8-honeycomb | {3[8]} | δ8 | hδ8 | qδ8 | 133 • 331 |
| Uniform 9-honeycomb | {3[9]} | δ9 | hδ9 | qδ9 | 152 • 251 • 521 |
| Uniform n-honeycomb | {3[n]} | δn | hδn | qδn | 1k2 • 2k1 • k21 |
This article is issued from Wikipedia. The text is available under the Creative Commons Attribution/Share Alike; additional terms may apply for the media files.