Quantum information

From Wikipedia, the free encyclopedia
For the journal with this title, see Historical Social Research.

In physics and computer science, quantum information is physical information that is held in the state of a quantum system. Quantum information is the basic entity that is studied in the burgeoning field of quantum information theory, and manipulated using the engineering techniques of quantum information processing. Much like classical information can be processed with digital computers, transmitted from place to place, manipulated with algorithms, and analyzed with the mathematics of computer science, so also analogous concepts apply to quantum information.

Quantum information

Quantum information differs strongly from classical information, epitomized by the bit, in many striking and unfamiliar ways. Among these are the following:

  • The unit of quantum information is the qubit. Unlike classical digital states (which are discrete), a qubit is continuous-valued, describable by a direction on the Bloch sphere. Despite being continuously valued in this way, a qubit is the smallest possible unit of quantum information. The reason for this indivisibility is due to the Heisenberg uncertainty principle: despite the qubit state being continuously-valued, it is impossible to measure the value precisely.
  • Despite the awkwardly-named no-teleportation theorem, qubits can be moved from one physical particle to another, by means of quantum teleportation. That is, qubits can be transported, independently of the underlying physical particle.
  • An arbitrary qubit can neither be copied, nor destroyed. This is the content of the no cloning theorem and the no-deleting theorem.
  • Although a single qubit can be transported from place to place (e.g. via quantum teleportation), it cannot be delivered to multiple recipients; this is the no-broadcast theorem, and is essentially implied by the no-cloning theorem.
  • Qubits can be changed, by applying linear transformations or quantum gates to them, to alter their state.
  • Classical bits may be combined with and extracted from configurations of multiple qubits, through the use of quantum gates. That is, two or more qubits can be arranged in such a way as to convey classical bits. The simplest such configuration is the Bell state, which consists of two qubits and four classical bits (i.e. requires two qubits and four classical bits to fully describe).
  • Quantum information can be moved about, in a quantum channel, analogous to the concept of a classical communications channel. Quantum messages have a finite size, measured in qubits; quantum channels have a finite channel capacity, measured in qubits per second.
  • Multiple qubits can be used to carry classical bits. Although n qubits can carry more than n classical bits of information, the greatest amount of classical information that can be retrieved is n. This is Holevo's theorem.
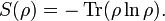  • Quantum information, and changes in quantum information, can be quantitatively measured by using an analogue of Shannon entropy, called the von Neumann entropy. Given a statistical ensemble of quantum mechanical systems with the density matrix \rho , it is given by S(\rho )=-\operatorname {Tr}(\rho \ln \rho ).\, Many of the same entropy measures in classical information theory can also be generalized to the quantum case, such as Holevo entropy and the conditional quantum entropy.
  • Quantum algorithms have a different computational complexity than classical algorithms. The most famous example of this is Shor's factoring algorithm, which does not have a polynomial time classical algorithm, but does have a polynomial time quantum algorithm. Other examples include Grover's search algorithm, where the quantum algorithm gives a quadratic speed-up over the best possible classical algorithm.
  • Quantum encryption allows unconditionally secure transmission of classical information, unlike classical encryption, which can always be broken in principle, if not in practice. (Note that certain subtle points are hotly debated).
  • Linear logic describes the logic of quantum information, in analogy to how classical logic works with classical bits. Linear logic is much like classical logic, except that Gentzen's rules for cloning are omitted. That is, entailment cannot be used to clone or delete logical premises, since qubits cannot be cloned or deleted.

The study of all of the above topics and differences comprises quantum information theory.

Quantum information theory

The theory of quantum information is a result of the effort to generalize classical information theory to the quantum world. Quantum information theory aims to investigate the following question:

How is information stored in a state of a quantum system?

As mentioned in the introduction, an arbitrary quantum state cannot be preciely converted in classical bits; this is the content of the no-teleportation theorem.

The information content of a message M can be measured in terms of the minimum number n of qubits needed to encode the message. Such a message M is encoded with n qubits and n2 classical bits that describe the relative arrangement of the n qubits. The qubit is the smallest possible unit of quantum information.

Quantum information can be transmitted through quantum channels, which do have a finite capacity. This is analogous to the classical case, where the noisy-channel coding theorem defines the maximum channel capacity of a classical communications channel. An important breakthrough for the theory of quantum information occurred when quantum error correction codes and fault-tolerant quantum computation schemes were discovered.

Quantum information can be manipulated and processed using quantum logic gates, in rough analog to the processing of classical information with digital circiuts.

Journals

Among the journals publishing new results in this field are

See also

References

  1. ↑ Bob Coecke, "Quantum Picturalism", (2009) Contemporary Physics vol 51, pp59-83. (ArXiv 0908.1787)

External links and references

General
Quantum communication
Quantum algorithms
Quantum complexity theory
Quantum computing models
Decoherence prevention
Physical implementations
Spin-based

This article is issued from Wikipedia. The text is available under the Creative Commons Attribution/Share Alike; additional terms may apply for the media files.