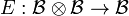Quantum Markov chain

From Wikipedia, the free encyclopedia

In mathematics, the quantum Markov chain is a reformulation of the ideas of a classical Markov chain, replacing the classical definitions of probability with quantum probability. Very roughly, the theory of a quantum Markov chain resembles that of a measure-many automata, with some important substitutions: the initial state is to be replaced by a density matrix, and the projection operators are to be replaced by positive operator valued measures.

More precisely, a quantum Markov chain is a pair 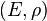$(E,\rho )$ with $\rho$ a density matrix and $E$ a quantum channel such that

$E:{\mathcal {B}}\otimes {\mathcal {B}}\to {\mathcal {B}}$

is a completely positive trace-preserving map, and 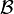${\mathcal {B}}$ a C^*-algebra of bounded operators. The pair must obey the quantum Markov condition, that

$\operatorname {Tr}\rho (b_{1}\otimes b_{2})=\operatorname {Tr}\rho E(b_{1},b_{2})$

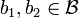for all $b_{1},b_{2}\in {\mathcal {B}}$ .

This article is issued from Wikipedia. The text is available under the Creative Commons Attribution/Share Alike; additional terms may apply for the media files.