Pyramid inch
The pyramid inch is a unit of measure claimed by pyramidologists to have been used in ancient times. Supposedly it was one twenty-fifth of a "sacred cubit", 1.00106 imperial inches, or 2.5426924 centimetres.[citation needed]
History
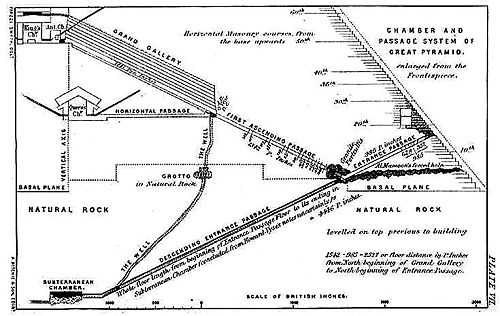
The first suggestion that the builders of the Great Pyramid of Giza used units of measure related to modern measures is attributed to Oxford astronomy professor John Greaves (1602–1652), who journeyed to Egypt in 1638 to make measurements of the pyramid. His findings were published in his Pyramidographia and under his name in an anonymous tract.[1] More than a century later, Greaves' measurements and additional measurements made by French engineers during Napoleon's expedition in Egypt, were studied by John Taylor (1781–1864). Taylor claimed that the measurements indicated that the ancients had used a unit of measure about 1/1000 greater than a modern British inch.[2] This was the origin of the "pyramid inch". Taylor regarded the "pyramid inch" to be 1/25 of the "sacred cubit" whose existence had earlier been postulated by Isaac Newton.[3] The principal argument was that the total length of the four sides of the pyramid would be 36524 (100 times the number of days in a year) if measured in pyramid inches. Taylor and his followers, who included the Astronomer Royal of Scotland Charles Piazzi Smyth (1819–1900),[4] also found numerous apparent coincidences between the measurements of the pyramids and the geometry of the earth and the solar system. They concluded that the British system of measures was derived from a far more ancient, if not divine, system. During the 19th and early 20th centuries, this theory played a significant role in the debates over whether Britain and the United States should adopt the metric system.[5]
The theory of Taylor and Smyth gained many eminent supporters and detractors during the following decades, but by the end of the 19th century it had lost most of its mainstream scientific support. The greatest blow to the theory was dealt by the great Egyptogist Flinders Petrie (1853–1942), whose father was a believer. When Petrie went to Egypt in 1880 to perform new measurements, he found that the pyramid was several feet smaller than previously believed, including the missing capstone. This so undermined the theory that Petrie rejected it, writing "there is no authentic example, that will bear examination, of the use or existence of any such measure as a ‘Pyramid inch,’ or of a cubit of 25.025 British inches."[6]
The value of 1.00106 British inches is calculated as 1/500,000,000 of the Earth's polar diameter. The pyramid inch now appears to have no significant scientific support. No direct evidence for it has ever been found, so pyramidologists argue from an increasing list of alleged numerical coincidences.
References
- ↑ J. Greaves [probably not the real author], The origin and antiquity of our English weights and measures discover'd: by their near agreement with such standards that are now found in one of the Egyptian pyramids: together with the explanation of divers lines therein heretofore measur'd (London: Printed for G. Sawbridge, 1706).
- ↑ John Taylor, The Great Pyramid, Why Was It Built? and Who Built It? (London, 1859).
- ↑ However Newton's value for this cubit was somewhat shorter; see Peter Tomkins, Secrets of the Great Pyramid (London: Allen Lane, 1971), p. 30–31.
- ↑ C. Piazzi Smyth, Our inheritance in the Great Pyramid, with photograph, map, and plates (London, 1864).
- ↑ E. M. Reisenauer, "The Battle of the Standards": Great Pyramid Metrology and British Identity, 1859-1890, The Historian 65, no. 4 (Summer 2003): 931–978; E. F. Cox, "The International Institute: First organized opposition to the metric system" Ohio History v. 68: PP. 54–83 .
- ↑ W. M. Flinders Petrie, The Pyramids and Temples of Gizeh (London, 1883), p189 .