Pulse compression
Pulse compression is a signal processing technique mainly used in radar, sonar and echography to increase the range resolution as well as the signal to noise ratio. This is achieved by modulating the transmitted pulse and then correlating the received signal with the transmitted pulse.[1]
Simple pulse
Signal description
The simplest signal a pulse radar can transmit is a sinusoidal pulse of amplitude,  and carrier frequency,
and carrier frequency, 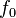 , truncated by a rectangular function of width,
, truncated by a rectangular function of width, 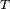 . The pulse is transmitted periodically, but that is not the main topic of this article; we will consider only a single pulse,
. The pulse is transmitted periodically, but that is not the main topic of this article; we will consider only a single pulse,  . If we assume the pulse to start at time
. If we assume the pulse to start at time 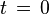 , the signal can be written the following way, using the complex notation:
, the signal can be written the following way, using the complex notation:
Range resolution
Let us determine the range resolution which can be obtained with such a signal. The return signal, written 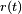 , is an attenuated and time-shifted copy of the original transmitted signal (in reality, Doppler effect can play a role too, but this is not important here.) There is also noise in the incoming signal, both on the imaginary and the real channel, which we will assume to be white and Gaussian (this generally holds in reality); we write
, is an attenuated and time-shifted copy of the original transmitted signal (in reality, Doppler effect can play a role too, but this is not important here.) There is also noise in the incoming signal, both on the imaginary and the real channel, which we will assume to be white and Gaussian (this generally holds in reality); we write  to denote that noise. To detect the incoming signal, matched filtering is commonly used. This method is optimal when a known signal is to be detected among an additive white Gaussian noise.
to denote that noise. To detect the incoming signal, matched filtering is commonly used. This method is optimal when a known signal is to be detected among an additive white Gaussian noise.
In other words, the cross-correlation of the received signal with the transmitted signal is computed. This is achieved by convolving the incoming signal with a conjugated and time-reversed version of the transmitted signal. This operation can be done either in software or with hardware. We write 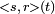 for this cross-correlation. We have:
for this cross-correlation. We have:
If the reflected signal comes back to the receiver at time  and is attenuated by factor
and is attenuated by factor 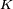 , this yields:
, this yields:
Since we know the transmitted signal, we obtain:
where  , the result of the intercorrelation between the noise and the transmitted signal. Function
, the result of the intercorrelation between the noise and the transmitted signal. Function  is the triangle function, its value is 0 on
is the triangle function, its value is 0 on ![\scriptstyle [-\infty ,\,-{\frac {1}{2}}]\,\cup \,[{\frac {1}{2}},\,+\infty ]](/2014-wikipedia_en_all_02_2014/I/media/9/7/2/6/97263a46e2f4f20f80df63bb91803b9b.png) , it increases linearly on
, it increases linearly on ![\scriptstyle [-{\frac {1}{2}},\,0]](/2014-wikipedia_en_all_02_2014/I/media/5/3/0/a/530a876a05ff66e0d4dbf1aceba64c30.png) where it reaches its maximum 1, and it decreases linearly on
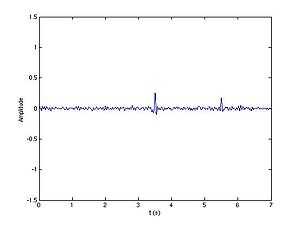
where it reaches its maximum 1, and it decreases linearly on ![\scriptstyle [0,\,{\frac {1}{2}}]](/2014-wikipedia_en_all_02_2014/I/media/a/f/f/8/aff8ada40777aac77a57230f93253d76.png) until it reaches 0 again. Figures at the end of this paragraph show the shape of the intercorrelation for a sample signal (in red), in this case a real truncated sine, of duration
until it reaches 0 again. Figures at the end of this paragraph show the shape of the intercorrelation for a sample signal (in red), in this case a real truncated sine, of duration  seconds, of unit amplitude, and frequency
seconds, of unit amplitude, and frequency 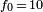 hertz. Two echoes (in blue) come back with a delay of 3 and 5 seconds, respectively, and have an amplitude equal to 0.5 and 0.3; those are just random values for the sake of the example. Since the signal is real, the intercorrelation is weighted by an additional 1⁄2 factor.
hertz. Two echoes (in blue) come back with a delay of 3 and 5 seconds, respectively, and have an amplitude equal to 0.5 and 0.3; those are just random values for the sake of the example. Since the signal is real, the intercorrelation is weighted by an additional 1⁄2 factor.
If two pulses come back (nearly) at the same time, the intercorrelation is equal to the sum of the intercorrelations of the two elementary signals. To distinguish one "triangular" envelope from that of the other pulse, it is clearly visible that the times of arrival of the two pulses must be separated by at least 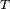 so that the maxima of both pulses can be separated. If this condition is not met, both triangles will be mixed together and impossible to separate.
so that the maxima of both pulses can be separated. If this condition is not met, both triangles will be mixed together and impossible to separate.
Since the distance travelled by a wave during 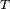 is
is 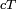 (where c is the speed of the wave in the medium), and since this distance corresponds to a round-trip time, we get:
(where c is the speed of the wave in the medium), and since this distance corresponds to a round-trip time, we get:
| Result 1 |
|---|
The range resolution with a sinusoidal pulse is  where where 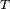 is the pulse Duration and, is the pulse Duration and,  , the speed of the wave. , the speed of the wave.
Conclusion: to increase the resolution, the pulse length must be reduced. |
| Before matched filtering | After matched filtering |
|---|---|
 If the targets are separated enough... |
 ...echoes can be distinguished. |
 If the targets are too close... |
 ...the echoes are mixed together. |
Required energy to transmit that signal
The instantaneous power of the transmitted pulse is 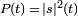 . The energy put into that signal is:
. The energy put into that signal is:
Similarly, the energy in the received pulse is 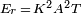 . If
. If  is the standard deviation of the noise, the signal-to-noise ratio (SNR) at the receiver is:
is the standard deviation of the noise, the signal-to-noise ratio (SNR) at the receiver is:
The SNR is proportional to pulse duration  , if other parameters are held constant. This introduces a tradeoff: increasing
, if other parameters are held constant. This introduces a tradeoff: increasing  improves the SNR, but reduces the resolution, and vice versa.
improves the SNR, but reduces the resolution, and vice versa.
Pulse compression by linear frequency modulation (or chirping)
Basic principles
How can one have a large enough pulse (to still have a good SNR at the receiver) without poor resolution? This is where pulse compression enters the picture. The basic principle is the following:
- a signal is transmitted, with a long enough length so that the energy budget is correct
- this signal is designed so that after matched filtering, the width of the intercorrelated signals is smaller than the width obtained by the standard sinusoidal pulse, as explained above (hence the name of the technique: pulse compression).
In radar or sonar applications, linear chirps are the most typically used signals to achieve pulse compression. The pulse being of finite length, the amplitude is a rectangle function. If the transmitted signal has a duration 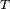 , begins at
, begins at 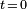 and linearly sweeps the frequency band
and linearly sweeps the frequency band 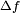 centered on carrier
centered on carrier  , it can be written:
, it can be written:
The chirp definition above means that the phase of the chirped signal (that is, the argument of the complex exponential), is the quadratic:
thus the instantaneous frequency is (by definition):
which is the intended linear ramp going from 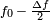 at
at 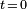 to
to 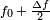 at
at 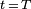 .
.
The relation of phase to frequency is often used in the other direction, starting with the desired 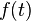 and writing the chirp phase via the integration of frequency:
and writing the chirp phase via the integration of frequency:
Cross-correlation between the transmitted and the received signal
As for the "simple" pulse, let us compute the cross-correlation between the transmitted and the received signal. To simplify things, we shall consider that the chirp is not written as it is given above, but in this alternate form (the final result will be the same):
Since this cross-correlation is equal (save for the  attenuation factor), to the autocorrelation function of
attenuation factor), to the autocorrelation function of  , this is what we consider:
, this is what we consider:
It can be shown[2] that the autocorrelation function of 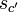 is:
is:
The maximum of the autocorrelation function of  is reached at 0. Around 0, this function behaves as the sinc (or cardinal sine) term. The −3 dB temporal width of that cardinal sine is more or less equal to
is reached at 0. Around 0, this function behaves as the sinc (or cardinal sine) term. The −3 dB temporal width of that cardinal sine is more or less equal to  . Everything happens as if, after matched filtering, we had the resolution that would have been reached with a simple pulse of duration
. Everything happens as if, after matched filtering, we had the resolution that would have been reached with a simple pulse of duration 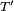 . For the common values of
. For the common values of 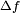 ,
, 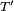 is smaller than
is smaller than 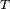 , hence the pulse compression name.
, hence the pulse compression name.
Since the cardinal sine can have annoying sidelobes, a common practice is to filter the result by a window (Hamming, Hann, etc.). In practice, this can be done at the same time as the adapted filtering by multiplying the reference chirp with the filter. The result will be a signal with a slightly lower maximum amplitude, but the sidelobes will be filtered out, which is more important.
| Result 2 |
|---|
The distance resolution reachable with a linear frequency modulation of a pulse on a bandwidth 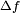 is: is: 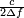 where where  is the speed of the wave. is the speed of the wave. |
| Definition |
|---|
Ratio 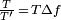 is the pulse compression ratio. It is generally greater than 1 (usually, its value is 20 to 30). is the pulse compression ratio. It is generally greater than 1 (usually, its value is 20 to 30). |
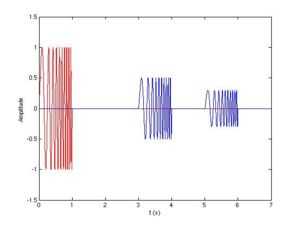 Before matched filtering |
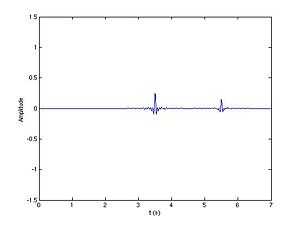 After matched filtering: the echoes are shorter in time. |
Improving the SNR through pulse compression
The energy of the signal does not vary during pulse compression. However, it is now located in the main lobe of the cardinal sine, whose width is approximately 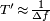 . If
. If 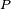 is the power of the signal before compression, and
is the power of the signal before compression, and 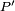 the power of the signal after compression, we have:
the power of the signal after compression, we have:
which yields:
Besides, the power of the noise does not change through intercorrelation since it is not correlated to the transmitted pulse (it is totally random). As a consequence:
| Result 3 |
|---|
After pulse compression, the power of the received signal can be considered as being amplified by 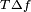 . This additional gain can be injected in the radar equation. . This additional gain can be injected in the radar equation. |
 Before matched filtering: the signal is hidden in noise |
 After matched filtering: echoes become visible. |
Pulse compression by phase coding
There are other means to modulate the signal. Phase modulation is a commonly used technique; in this case, the pulse is divided in 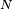 time slots of duration
time slots of duration 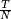 for which the phase at the origin is chosen according to a pre-established convention. For instance, it is possible not to change the phase for some time slots (which comes down to just leave the signal as it is, in those slots) and de-phase the signal in the other slots by
for which the phase at the origin is chosen according to a pre-established convention. For instance, it is possible not to change the phase for some time slots (which comes down to just leave the signal as it is, in those slots) and de-phase the signal in the other slots by  (which is equivalent of changing the sign of the signal). The precise way of choosing the sequence of
(which is equivalent of changing the sign of the signal). The precise way of choosing the sequence of 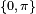 phases is done according to a technique known as Barker codes. It is possible to code the sequence on more than two phases (polyphase coding). As with a linear chirp, pulse compression is achieved through intercorrelation.
phases is done according to a technique known as Barker codes. It is possible to code the sequence on more than two phases (polyphase coding). As with a linear chirp, pulse compression is achieved through intercorrelation.
The advantages[3] of the Barker codes are their simplicity (as indicated above, a  de-phasing is a simple sign change), but the pulse compression ratio is lower than in the chirp case and the compression is very sensitive to frequency changes due to the Doppler effect if that change is larger than
de-phasing is a simple sign change), but the pulse compression ratio is lower than in the chirp case and the compression is very sensitive to frequency changes due to the Doppler effect if that change is larger than  .
.
Notes
- ↑ J. R. Klauder, A. C, Price, S. Darlington and W. J. Albersheim, ‘The Theory and Design of Chirp Radars,” Bell System Technical Journal 39, 745 (1960).
- ↑ Achim Hein, Processing of SAR Data: Fundamentals, Signal Processing, Interferometry, Springer, 2004, ISBN 3-540-05043-4, pages 38 to 44. Very rigorous demonstration of the autocorrelation function of a chirp. The author works with real chirps, hence the factor of 1⁄2 in his book, which is not used here.
- ↑ J.-P. Hardange, P. Lacomme, J.-C. Marchais, Radars aéroportés et spatiaux, Masson, Paris, 1995, ISBN 2-225-84802-5, page 104. Available in English: Air and Spaceborne Radar Systems: an introduction, Institute of Electrical Engineers, 2001, ISBN 0-85296-981-3

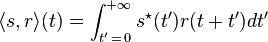
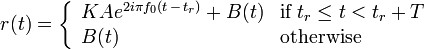
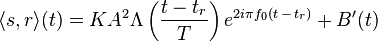
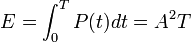
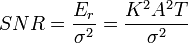
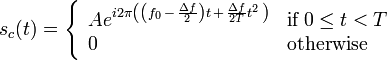
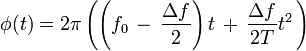
![f(t)={\frac {1}{2\pi }}\left[{\frac {d\phi }{dt}}\right]_{t}=f_{0}-{\frac {\Delta f}{2}}+{\frac {\Delta f}{T}}t](/2014-wikipedia_en_all_02_2014/I/media/3/2/6/6/3266298f20ba66eb6e810258e1f05db2.png)
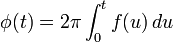


![\langle s_{{c'}},s_{{c'}}\rangle (t)=A^{2}T\Lambda \left({\frac {t}{T}}\right){\mathrm {sinc}}\left[\pi \Delta ft\Lambda \left({\frac {t}{T}}\right)\right]e^{{2i\pi f_{0}t}}](/2014-wikipedia_en_all_02_2014/I/media/a/9/4/b/a94b206824f9cdafbead30d614e43379.png)
 )
)