Proper map

From Wikipedia, the free encyclopedia

This article is about the concept in topology. For the concept in convex analysis, see proper convex function.

In mathematics, a continuous function between topological spaces is called proper if inverse images of compact subsets are compact. In algebraic geometry, the analogous concept is called a proper morphism.

Definition

A function f : X → Y between two topological spaces is proper if the preimage of every compact set in Y is compact in X.

There are several competing descriptions. For instance, a continuous map f is proper if it is a closed map and the pre-image of every point in Y is compact. The two definitions are equivalent if Y is compactly generated and Hausdorff. For a proof of this fact see the end of this section. More abstractly, f is proper if f is universally closed, i.e. if for any topological space Z the map

f × id_Z: X × Z → Y × Z

is closed. These definitions are equivalent to the previous one if X is Hausdorff and Y is locally compact Hausdorff.

An equivalent, possibly more intuitive definition when X and Y are metric spaces is as follows: we say an infinite sequence of points {p_i} in a topological space X escapes to infinity if, for every compact set S ⊂ X only finitely many points p_i are in S. Then a continuous map f : X → Y is proper if and only if for every sequence of points {p_i} that escapes to infinity in X, {f(p_i)} escapes to infinity in Y.

This last sequential idea looks like being related to the notion of sequentially proper, see a reference below.

Proof of fact

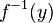Let $f:X\to Y$ be a continuous closed map, such that $f^{{-1}}(y)$ is compact (in X) for all 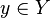$y\in Y$ . Let $K$ be a compact subset of $Y$ . We will show that $f^{{-1}}(K)$ is compact.

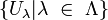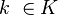Let $\{U_{{\lambda }}\vert \lambda \ \in \ \Lambda \}$ be an open cover of $f^{{-1}}(K)$ . Then for all $k\ \in K$ this is also an open cover of 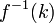$f^{{-1}}(k)$ . Since the latter is assumed to be compact, it has a finite subcover. In other words, for all 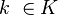$k\ \in K$ there is a finite set 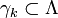$\gamma _{k}\subset \Lambda$ such that $f^{{-1}}(k)\subset \cup _{{\lambda \in \gamma _{k}}}U_{{\lambda }}$ . 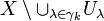The set $X\setminus \cup _{{\lambda \in \gamma _{k}}}U_{{\lambda }}$ is closed. Its image is closed in Y, because f is a closed map. Hence the set

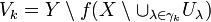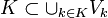$V_{k}=Y\setminus f(X\setminus \cup _{{\lambda \in \gamma _{k}}}U_{{\lambda }})$ is open in Y. It is easy to check that $V_{k}$ contains the point $k$ . Now $K\subset \cup _{{k\in K}}V_{k}$ and because K is assumed to be compact, there are finitely many points 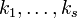$k_{1},\dots ,k_{s}$ such that 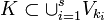$K\subset \cup _{{i=1}}^{s}V_{{k_{i}}}$ . Furthermore the set $\Gamma =\cup _{{i=1}}^{s}\gamma _{{k_{i}}}$ is a finite union of finite sets, thus $\Gamma$ is finite.

Now it follows that 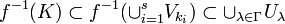$f^{{-1}}(K)\subset f^{{-1}}(\cup _{{i=1}}^{s}V_{{k_{i}}})\subset \cup _{{\lambda \in \Gamma }}U_{{\lambda }}$ and we have found a finite subcover of $f^{{-1}}(K)$ , which completes the proof.

Properties

A topological space is compact if and only if the map from that space to a single point is proper.
Every continuous map from a compact space to a Hausdorff space is both proper and closed.
If f : X → Y is a proper continuous map and Y is a compactly generated Hausdorff space (this includes Hausdorff spaces which are either first-countable or locally compact), then f is closed.^[1]

Generalization

It is possible to generalize the notion of proper maps of topological spaces to locales and topoi, see (Johnstone 2002).

References

Bourbaki, Nicolas (1998), General topology. Chapters 5--10, Elements of Mathematics, Berlin, New York: Springer-Verlag, ISBN 978-3-540-64563-4, MR 1726872
Johnstone, Peter (2002), Sketches of an elephant: a topos theory compendium, Oxford: Oxford University Press, ISBN 0-19-851598-7 , esp. section C3.2 "Proper maps"

Brown, Ronald (2006), Topology and groupoids, N. Carolina: Booksurge, ISBN 1-4196-2722-8 , esp. p. 90 "Proper maps" and the Exercises to Section 3.6.

Brown, R. "Sequentially proper maps and a sequential compactification", J. London Math Soc. (2) 7 (1973) 515-522.

↑ Palais, Richard S. (1970). "When proper maps are closed". Proc. Amer. Math. Soc. 24: 835–836.

This article is issued from Wikipedia. The text is available under the Creative Commons Attribution/Share Alike; additional terms may apply for the media files.